8.2 Räumliche Leiterschleife
Als weiteres Testbeispiel bietet sich eine einfache, räumliche Leiterschleife
an: Das Simulationsgitter ist dargestellt in Abb. 8.6(a) als
Drahtmodell, und der Aufbau der Strukur ist deutlicher erkennbar in
Abb. 8.6(b), der Querschnitt des Leiters beträgt
1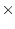 1
1
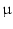 m
m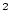 , die
Leiterschleife findet in einem Quader mit den Ausmaßen
9
, die
Leiterschleife findet in einem Quader mit den Ausmaßen
9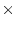 9
9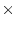 3
3
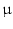 m
m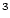 Platz. Abbildung 8.7 zeigt
wiederum das Konvergenzverhalten der Monte Carlo Methode; das Resultat für
Platz. Abbildung 8.7 zeigt
wiederum das Konvergenzverhalten der Monte Carlo Methode; das Resultat für 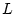 =21.91 pH. Die Vektorpotenzialmethode liefert als Wert der
Selbstinduktivität 21.86 pH. Zusätzlich ist der Betrag der
Stromdichteverteilung in Abb. 8.8 dargestellt. Die Maxima der
Stromdichte treten in den inneren Ecken der Leiterschleife auf, die Minima an
den äußeren Ecken (blau). Die Verteilung des Vektorpotenzials wird in
Abb. 8.9 gezeigt. Neben der Größe erfolgt durch die Farbe der
Kegel die Zuordnung der Maxima (rot) und Minima (blau).
Die Darstellung des magnetischen Felds (Abb. 8.10) auf der
Leiteroberfläche erfolgt wiederum mit Kegel. Abschließend ist noch die
Potenzialverteilung (Abb. 8.11) mit dem Gitter gemeinsam zu sehen.
=21.91 pH. Die Vektorpotenzialmethode liefert als Wert der
Selbstinduktivität 21.86 pH. Zusätzlich ist der Betrag der
Stromdichteverteilung in Abb. 8.8 dargestellt. Die Maxima der
Stromdichte treten in den inneren Ecken der Leiterschleife auf, die Minima an
den äußeren Ecken (blau). Die Verteilung des Vektorpotenzials wird in
Abb. 8.9 gezeigt. Neben der Größe erfolgt durch die Farbe der
Kegel die Zuordnung der Maxima (rot) und Minima (blau).
Die Darstellung des magnetischen Felds (Abb. 8.10) auf der
Leiteroberfläche erfolgt wiederum mit Kegel. Abschließend ist noch die
Potenzialverteilung (Abb. 8.11) mit dem Gitter gemeinsam zu sehen.
Abbildung 8.6:
Elementlinien der Leiterschleife (a) und Geometrie mit Gitter (b)
![\centerline{%
\begin{minipage}[t]{0.470\textwidth}\centerline{\hss\resizebox{\li...
...egraphics[{clip}]{Knotffem2}}\hss}
\vspace{5pt}\centerline{(b)}\end{minipage}}](img533.png) |
Abbildung 8.7:
Darstellung der berechneten Selbstinduktivität der
Leiterschleife in Abhängigkeit der Stichprobenanzahl
![\begin{figure}{\resizebox{0.72\textwidth}{!}{\includegraphics[{}]{MCconvKnot}}}\end{figure}](img534.png) |
Abbildung 8.8:
Stromdichteverteilung der Leiterschleife
![\begin{figure}{\resizebox{0.68\textwidth}{!}{\includegraphics[{clip}]{knotfcurr}}}\end{figure}](img535.png) |
Abbildung 8.9:
Darstellung des Vektorpotenzials: Die Kegel geben die Größe und Richtung des
Vektorpotenzials an.
![\begin{figure}{\resizebox{0.71\textwidth}{!}{\includegraphics[{clip}]{gdeKnotvp}}}\end{figure}](img536.png) |
Abbildung 8.10:
Magnetisches Feld und elektrisches Potenzial auf derLeiteroberfläche:
Das magnetische Feld verläuft tangential.
![\begin{figure}{\resizebox{0.83\textwidth}{!}{\includegraphics[{clip}]{2b}}}\end{figure}](img537.png) |
Abbildung 8.11:
Potenzialverteilung der Leiterschleife
![\begin{figure}{\resizebox{0.86\textwidth}{!}{\includegraphics[{clip}]{knotfpot}}}\end{figure}](img538.png) |
C. Harlander: Numerische Berechnung von Induktivitšten in dreidimensionalen Verdrahtungsstrukturen
![\begin{figure}{\resizebox{0.72\textwidth}{!}{\includegraphics[{}]{MCconvKnot}}}\end{figure}](img534.png)
![\begin{figure}{\resizebox{0.71\textwidth}{!}{\includegraphics[{clip}]{gdeKnotvp}}}\end{figure}](img536.png)
![\begin{figure}{\resizebox{0.83\textwidth}{!}{\includegraphics[{clip}]{2b}}}\end{figure}](img537.png)