8.3 Spiralinduktor

Anhand eines Induktors wird der Einfluss des Substrats in Hinblick auf die Induktivität im statischen Fall untersucht. Die Leitfähigkeiten der verwendeten Materialien sind in Tab. 8.2 aufgelistet.

**Tabelle 8.2:** Materialparameter
$\begin{tabular}{l l l}\hline &$\gamma_i$&Leitf''ahigkeit \rule[-2.5mm]{0pt}{3.7... ...cdot 10^{-8}$\\ Metall & $\gamma_M$&4.167$\cdot 10^{7}$\\ \hline \end{tabular}$

**Abbildung 8.12:** Geometrie des planaren Induktors: Dimensionen in $\protect{\mbox{{\usefont{U}{eur}{m}{n}\char22}}}$ m
$\begin{figure}{\resizebox{0.8\textwidth}{!}{\includegraphics[{angle=-90}]{geomBen8}}}\end{figure}$

**Abbildung 8.13:** Schichtaufbau: Schematische Darstellung der Struktur, Abmessungen in $\protect{\mbox{{\usefont{U}{eur}{m}{n}\char22}}}$ m
$\begin{figure}{\resizebox{0.79\textwidth}{!}{\includegraphics[{}]{schicht8}}}\end{figure}$

Abbildung 8.12 gibt die Geometrie des Induktors wieder, Abb. 8.13 verdeutlicht den Schichtaufbau. Die Spule ist durch eine Oxidschicht der Höhe 1.5 $\protect{\mbox{{\usefont{U}{eur}{m}{n}\char22}}}$ m von Substrat 2 isoliert. Die Ergebnisse der Berechnung der Selbstinduktivität sind in Tab. 8.3 aufgelistet. In der ersten Zeile stehen die Simulationsergebnisse für isolierendes Siliziumsubstrat/Siliziumoxid. Die Resultate geben Aufschluss über die Veränderungen der Induktivität aufgrund der veränderten Potenzialverteilung zufolge der Leitfähigkeiten im Substrat und im Oxid. Im statischen Fall besteht kein Unterschied zwischen der Berücksichtigung der Leitfähigkeit der beiden Substrate und deren Vernachlässigung.

**Tabelle 8.3:** Resultate der Induktivitätsberechnung: Monte Carlo Methode versus Vektorpotenzialmethode
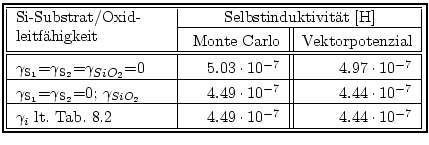
$% latex2html id marker 15762 \fbox{% \begin{minipage}{0.582\textwidth} \begin{t... ... $4.49\cdot10^{-7}$\ & $4.44\cdot10^{-7}$\\ \hline \end{tabular}\end{minipage}}$

Die folgenden Abbildungen geben Verteilungen des elektrischen Potenzials, sowie der Beträge der elektrischen Stromdichte, des magnetischen Vektorpotenzials und der magnetischen Flussdichte wieder. Abbildung 8.14, Abb. 8.15 und Abb. 8.16 sind Simulationsergebnisse auf ideal isolierendem Oxid. Weitere Abbildungen zeigen die veränderten Verhältnisse aufgrund der Leitfähigkeit $\gamma_{\protect\makebox{\footnotesize {$SiO_2$}}}$ des Oxids nach Tab. 8.2 auf: So ist z.B. die Potenzialverteilung in Abb. 8.18 etwas verschmiert ins leitfähige Oxid fortgesetzt. Zwischen den beiden Stromdichteverteilungen lassen sich optisch keine Abweichungen erkennen. Wie erwartet tritt die höchste Stromdichte an inneren Knickpunkten des Polygons auf. An den beiden Vektorpotenzialverteilungen ist jeweils der starke Einfluss der fünf parallelen Windungen bemerkenswert, der ein Maximum des Betrags des Vektorpotenzials in den mittleren Windungen bewirkt.

Abbildung 8.17 zeigt die starke Abhängigkeit des CG-Verfahrens von der Dicke des Spiralinduktors. In dieser Abbildung ist die Anzahl der Iterationen dargestellt, die notwendig ist, um das Gleichungssystem für den Spiralinduktor auf idealem Oxid zu lösen. Dabei sind für drei Fälle (Metallhöhe multipliziert mit Faktor 1, 10 und 100) jeweils knapp 6000 aktive Knoten zur Diskretisierung verwendet worden. Ein Schluss aus dieser Abbildung ist, dass lange, sehr dünne Schichten nicht nur hohe Ansprüche an die Gittergeneratoren stellen, sondern auch die Methode der Finiten Elemente zunehmend ineffizient machen.

**Abbildung 8.14:** Potenzialverteilung des Spiralinduktors auf idealem Oxid
$\begin{figure}{\resizebox{0.8\textwidth}{!}{\includegraphics[{}]{Ipotinductor}}}\end{figure}$

**Abbildung 8.15:** Stromdichteverteilung des Spiralinduktors auf idealem Oxid
$\begin{figure}{\resizebox{0.8\textwidth}{!}{\includegraphics[{}]{Icurrinductor}}}\end{figure}$

**Abbildung 8.16:** Vektorpotenzialverteilung auf dem Spiralinduktor
$\begin{figure}{\resizebox{0.8\textwidth}{!}{\includegraphics[{}]{Ivecinductor}}}\end{figure}$

**Abbildung 8.17:** Konvergenzverhalten des CG-Verfahrens abhängig von der Metalldicke des Spiralinduktors: Knapp 6000 aktive Knoten werden zur Diskretisierung des Spiralinduktors über idealem Oxid verwendet.
$\begin{figure}{\resizebox{0.72\textwidth}{!}{\includegraphics[{}]{iterate}}}\end{figure}$

**Abbildung 8.18:** Potenzialverteilung des Spiralinduktors auf dem Oxid mit der Leitfähigkeit $\gamma_{\protect\makebox{\footnotesize {$SiO_2$}}}$ laut Tab. 8.2
$\begin{figure}{\resizebox{0.82\textwidth}{!}{\includegraphics[{}]{Spotinductor}}}\end{figure}$

**Abbildung 8.19:** Stromdichteverteilung des Spiralinduktors auf dem Oxid mit der Leitfähigkeit $\gamma_{\protect\makebox{\footnotesize {$SiO_2$}}}$ laut Tab. 8.2
$\begin{figure}{\resizebox{0.82\textwidth}{!}{\includegraphics[{}]{Scurrinductor}}}\end{figure}$

**Abbildung 8.20:** Vektorpotenzialverteilung des Spiralinduktors auf dem Oxid mit der Leitfähigkeit $\gamma_{\protect\makebox{\footnotesize {$SiO_2$}}}$ laut Tab. 8.2
$\begin{figure}{\resizebox{0.82\textwidth}{!}{\includegraphics[{}]{Svecinductor}}}\end{figure}$