B. Analytische Formeln für parallele, rechteckige Leiter

In [41] sind analytische Lösungen für Selbst- und Gegeninduktivitäten von Kombinationen bestehend aus parallelen, rechteckigen Leitern mit konstanter Stromdichte angegeben. Die Selbstinduktivität eines rechteckigen Leiters der Länge $l$ mit dem Querschnitt $a\cdot{}b$ ist

$$L=\frac{\protect{\mbox{{\usefont{U}{eur}{m}{n}\char22}}}}{4{\pi}a... ...^{l} \frac{1}{\sqrt{(x-x')^2+(y-y')^2+(z-z')^2}} \mathrm{dz' dy' dx' dz dy dx},$$ (B.1)

wobei der Term im Nenner $a^2b^2$ von der Stromdichte des Leiters herrührt. Zur Berechnung der Gegeninduktivität müssen nur die Grenzen für die Integration entsprechend abgeändert werden. Der analytische Ausdruck in (B.1) läßt sich durch Ausnützung der Symmetrie nach Integration folgendermaßen schreiben:

$$L=\frac{2\protect{\mbox{{\usefont{U}{eur}{m}{n}\char22}}}}{{\pi}a^2b^2}\Bigg[\Bigg[\Bigg[f(x,y,z)\Bigg]_{x=0}^{a}\Bigg]_{y=0}^{b}\Bigg]_{z=0}^{l}$$ (B.2)

mit der Funktion

$$f(x,y,z)=x\big(\frac{y^2z^2}{4}-\frac{y^4}{24}-\frac{z^4}{24}\big) \ln\bigg(\frac{x+\sqrt{x^2+y^2+z^2}}{\sqrt{y^2+z^2}}\bigg)$$

$$+y\big(\frac{x^2z^2}{4}-\frac{x^4}{24}-\frac{z^4}{24}\big) \ln\bigg(\frac{y+\sqrt{x^2+y^2+z^2}}{\sqrt{x^2+z^2}}\bigg)$$

$$+z\big(\frac{x^2y^2}{4}-\frac{x^4}{24}-\frac{y^4}{24}\big) \ln\bigg(\frac{z+\sqrt{x^2+y^2+z^2}}{\sqrt{x^2+y^2}}\bigg)$$

$$+\frac{1}{60}\big(x^4+y^4+z^4-3x^2y^2-3y^2z^2-3z^2x^2\big)\sqrt{x^2+y^2+z^2}$$

$$-\frac{xyz^3}{6}\arctan\frac{xy}{z\sqrt{x^2+y^2+z^2}} -\frac{xy^3z}{6}\arctan\frac{xz}{y\sqrt{x^2+y^2+z^2}}$$

$$-\frac{x^3yz}{6}\arctan\frac{yz}{x\sqrt{x^2+y^2+z^2}},$$

sowie

$$\Bigg[\Bigg[\Bigg[f(x,y,z)\Bigg]_{x=q_2}^{q_1}\Bigg]_{y=r_2}^{r_1... ...equiv\sum_{i=1}^2\sum_{j=1}^2\sum_{k=1}^2 \big(-1\big)^{i+j+k+1}f(q_i,r_j,s_k).$$

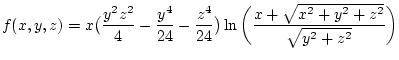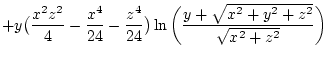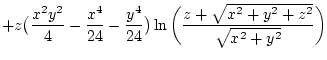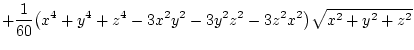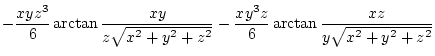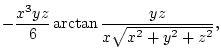Für Rechteckleiter mit einem Verhältnis von Dicke zu Breite $b/a$ kleiner als 0.1 ist in [41] auch eine genügend genaue Näherungsformel zu finden.

Basierend auf [41] ist in [39] eine computergerechtere Formulierung angegeben, die auch die Genauigkeit für lange, dünne Leiter verbessert.