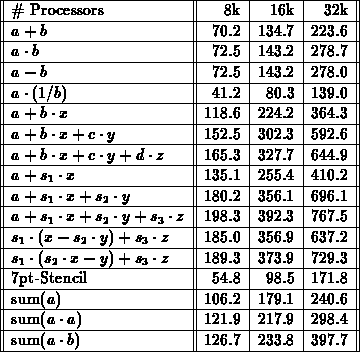
Tabelle: Arithmetische Operationen auf der CM-2 auf einem Tensor-Produkt-Gitter mit
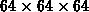 -Punkten. Werte in Megaflops,
Zeitmittelung über
-Punkten. Werte in Megaflops,
Zeitmittelung über 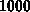 Berechnungen.
Berechnungen.




Die Connection Machine (CM) ist eine Realisierung eines
massiv-datenparallelen Computers. Die CM arbeitet gleichartige
Befehle auf einem großen gleichartigen
Datensatz gleichzeitig ab (SIMD-Architektur).
Eine fundiert-kritische Betrachtung der CM-2
und der vorhandenen Software dieser Maschine findet sich
z.B. in [91].

Tabelle: Arithmetische Operationen auf der CM-2 auf einem Tensor-Produkt-Gitter
mit 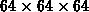 -Punkten. Werte in Megaflops,
Zeitmittelung über
-Punkten. Werte in Megaflops,
Zeitmittelung über 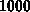 Berechnungen.
Berechnungen.
Zur Abschätzung der arithmetischen Leistungsfähigkeit wurde eine Menge sogenannter Benchmarks auf der Maschine CM-2 gestartet und Resultate in verschiedenen Prozessorkonfigurationen gewonnen. Die Konfigurationen entsprechen dreidimensionalen Tensor-Produkt-Gittern verschiedener Dimension. Die Anzahl der allozierten physikalischen Prozessoren ist 8192 (8k), 16384 (16k) und 32768 (32k).
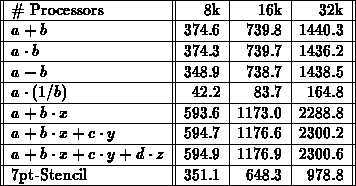
Tabelle: Eine Untermenge von Operationen gemäß Tabelle 6.4.
Benutzung eines speziellen Datenformates auf der CM-2 (,,Slicewise Data``)
und Überlappung von arithmetischer Operation mit
Datenkommunikation bei der 7-Stern-Berechnung ( pt-Stencil).
Werte in Megaflops, Zeitmittelung über
pt-Stencil).
Werte in Megaflops, Zeitmittelung über 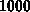 Berechnungen.
Berechnungen.
Aus Tabelle 6.4 und 6.5 ist die Eigenschaft
der Skalierbarkeit der Maschine zu erkennen. Diese Eigenschaft kommt natürlich
nur bei genügend großen Datenmengen zum Tragen.
Die Skalierbarkeit der Maschine wird durch das Konzept virtueller
Prozessoren realisiert. Das bedeutet, daß bei einer Gitterpunktanzahl,
die größer als die Anzahl der Prozessoren ist, mehrere Punkte einem
physikalischen Prozessor zugewiesen werden.
Umgekehrt emuliert ein physikalischer Prozessor
mehrere virtuelle Prozessoren. Die virtuellen Prozessoren
können die ihnen zugewiesenen Berechnungen nur seriell abarbeiten.
Für die in den Tabellen 6.4 und 6.5
angegebenen Berechnungen und Prozessorauslegungen ergibt sich sinngemäß
ein VPR (Virtual Processor Ratio - das Verhältnis zwischen virtuellen
und physikalischen Prozessoren) von 32 bei 8k Prozessoren, 16 bei 16k
Prozessoren und 8 bei 32k Prozessoren. Genaue Zeitmessungen ergaben,
daß die Berechnungszeiten nichtlinear mit dem VPR
zusammenhängen [59].
Die getesteten arithmetischen Operationen sind
verschiedene Linearkombinationen von Vektoren, die in den
iterativen Gleichungslösern auftreten. Diese erfordern keine
Interprozessor-Kommunikation. Die Ausführungsgeschwindigkeit
dieser Operationen hängt nur von den Einzelprozessoren ab, die
recht langsam sind
(Taktfrequenz kleiner als 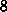 Mhz).
Der tatsächlich begrenzende Faktor dieser lokalen Berechnungen
ist jedoch die Busbandbreite zwischen lokalem Speicher und
den Einzelprozessoren.
Mhz).
Der tatsächlich begrenzende Faktor dieser lokalen Berechnungen
ist jedoch die Busbandbreite zwischen lokalem Speicher und
den Einzelprozessoren.
Operationen, die Interprozessor-Kommunikation benötigen, sind
das Inprodukt (globale Kommunikation) und die
Matrix-Vektor-Multiplikation (lokale Kommunikation
gemäß der  -Punkt-Diskretisierung).
Die Benchmarks in Tabelle 6.4
(die Inprodukt-Operation war im Slicewise-Format zur Zeit der
Untersuchung nicht verfügbar) zeigen, daß das Inprodukt
keineswegs der Flaschenhals im Datenfluß
ist. Dieser Flaschenhals ist vielmehr die lokale
Matrix-Vektormultiplikation. Grund für die langsame
Geschwindigkeit der 7-Stern-Operation (7-pt-Stencil) ist,
daß der Compiler der CM-2
die Parallelität der Operation nicht optimal ausnützt
und den Datenaustausch mit den
-Punkt-Diskretisierung).
Die Benchmarks in Tabelle 6.4
(die Inprodukt-Operation war im Slicewise-Format zur Zeit der
Untersuchung nicht verfügbar) zeigen, daß das Inprodukt
keineswegs der Flaschenhals im Datenfluß
ist. Dieser Flaschenhals ist vielmehr die lokale
Matrix-Vektormultiplikation. Grund für die langsame
Geschwindigkeit der 7-Stern-Operation (7-pt-Stencil) ist,
daß der Compiler der CM-2
die Parallelität der Operation nicht optimal ausnützt
und den Datenaustausch mit den 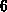 Nachbarn sequentiell
durchführt. Die optimierte Stencil-Routine in
der Tabelle 6.5 besitzt diese Einschränkung
nicht und beruht auf der optimalen Ausnützung aller
in der CM-2 zur Verfügung stehenden Kommunikationswege
(,,wires``). Die Stencil-Routine ist ca.
Nachbarn sequentiell
durchführt. Die optimierte Stencil-Routine in
der Tabelle 6.5 besitzt diese Einschränkung
nicht und beruht auf der optimalen Ausnützung aller
in der CM-2 zur Verfügung stehenden Kommunikationswege
(,,wires``). Die Stencil-Routine ist ca. 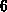 mal schneller.
mal schneller.
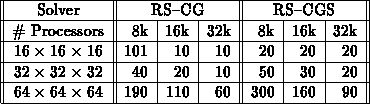
Tabelle 6.6: Test der RS-CG- and RS-CGS-Verfahren auf der CM-2.
Lösung der Laplacegleichung auf dem Einheitswürfel in
doppelter Genauigkeit.
Auf der Abszisse sind die Anzahl der Prozessoren
aufgetragen, auf der Ordinate die Dimensionen
der Tensor-Produkt-Gitter. Werte in  .
.
Neben arithmetischen Grundoperationen
(BLAS - Basic Linear Algebra Subprograms)
wurden auch die linearen Gleichungslöser, die
in der CM-2-Version von MINIMOS verwendet werden,
getestet. Als Testproblem dient die Laplacegleichung
im Einheitswürfel mit gemischten
Dirichlet-Neumann-Randbedingungen, als Zahlenformat
das Punkt-Format (pointwise format)
mit doppelter Genauigkeit. Drei Gitterkonfigurationen
(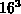 ,
, 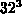 ,
, 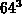 ) und drei
Prozessor-Allokationen (
) und drei
Prozessor-Allokationen (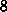 k,
k, 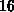 k
k 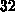 k) wurden
gemessen. Die Resultate findet man in Tabelle 6.6.
Für das
k) wurden
gemessen. Die Resultate findet man in Tabelle 6.6.
Für das 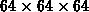 -Gitter und
-Gitter und 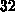 k Prozessoren
errechnet sich eine Megaflop-Rate von
k Prozessoren
errechnet sich eine Megaflop-Rate von 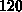 für
das RS-CGS-Verfahren, das einschließlich
des Abbruchkriteriums
für
das RS-CGS-Verfahren, das einschließlich
des Abbruchkriteriums 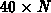 arithmetische Operationen
pro Iteration benötigt. Ähnliche Werte erhält man für
das RS-CG-Verfahren.
In erster Linie sind die
arithmetische Operationen
pro Iteration benötigt. Ähnliche Werte erhält man für
das RS-CG-Verfahren.
In erster Linie sind die 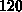 -Megaflops des
-Megaflops des  -Punkt-Sterns
(siehe Tabelle 6.4) für diese enttäuschend
langsame Rechengeschwindigkeit verantwortlich.
Es ist deutlich zu sehen, daß im Fall von VPR=
-Punkt-Sterns
(siehe Tabelle 6.4) für diese enttäuschend
langsame Rechengeschwindigkeit verantwortlich.
Es ist deutlich zu sehen, daß im Fall von VPR=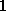 (das
(das 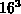 -Gitter)
die Rechenleistung nicht mit der Prozessorzahl skaliert.
-Gitter)
die Rechenleistung nicht mit der Prozessorzahl skaliert.
Zur Illustration der tatsächlichen Leistungsfähigkeit
des Programms MINIMOS auf der CM-2 wurden die
Beispiele MOSFET-1 und MOSFET-2
(siehe Abschnitt 5.4
im Kapitel 5) simuliert.
Resultate mit Iterationszahlen und
Rechenzeiten für die Poissongleichung (I-PO, T-PO),
Elektronenstrom-Kontinuitätsgleichung (I-EL, T-EL) und
Löcherstrom-Kontinuitätsgleichung (I-HO,T-HO) für
beiden Beispiele finden sich in den
Tabellen 6.7 (MOSFET-1) und 6.8
(MOSFET-2).
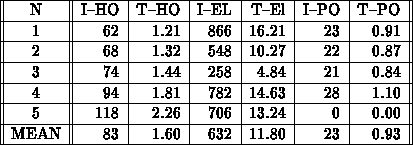
Tabelle 6.7: Gummel-Algorithmus. Zeitmessung und Iterationszahlen von MOSFET-1.
Beide Simulationen wurden mit 16k allozierten Prozessoren
und mit doppelter Genauigkeit vorgenommen.
Die Zeitmessungen besorgte eine Timing-Routine der
CM-2, die die CM-busy-time mißt und eine Genauigkeit
von einer Mikrosekunde besitzt.
Die Gitterkonfiguration von MOSFET-1 ist
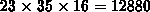 . Die CM-2 hat daher
ein VPR von eins.
. Die CM-2 hat daher
ein VPR von eins.
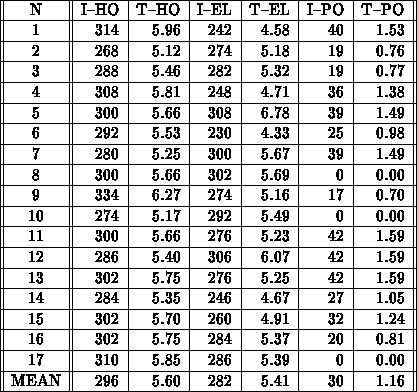
Tabelle 6.8: Gummel-Algorithmus. Zeitmessung und Iterationszahlen von MOSFET-2.
Die Kontinuitätsgleichung der Elektronen benötigt
die meiste CPU-Zeit (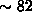 %). Verglichen
mit dem ICCG(0) und dem ILU-CGS-Gleichungslöser der
seriellen Implementation benötigt die parallele Implementation
%). Verglichen
mit dem ICCG(0) und dem ILU-CGS-Gleichungslöser der
seriellen Implementation benötigt die parallele Implementation



Eine Cray-2 mit einer vektorisierten
ICCG- und ILU-CGS-Implementation durch die
Hyperebenen-Methode schaffte das gleiche Beispiel
ca. viermal so schnell. Dieses ungünstige Resultat
wird nicht zuletzt durch die geringe Gitterpunktanzahl
verursacht.
Nicht viel günstiger sind die Resultate von MOSFET-2.
Dieser Simulation
benötigt ein Rechengitter von
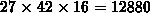 .
Die CM-2 ist ca.
.
Die CM-2 ist ca. 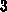 mal langsamer als die Cray-2, und mehr als
mal langsamer als die Cray-2, und mehr als
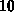 mal langsamer als der Fujitsu VP200 Supercomputer.
mal langsamer als der Fujitsu VP200 Supercomputer.



