14.3 Inverse Modeling and Results

Two points from the measurements in [95] were ignored since they were above the implanted dose. All measurements were viewed as one vector $m$. Let $s$ be the vector of simulation results depending on the parameters $p$ to be identified. The objective function $f(p)$ to be minimized was the quadratic mean of the element-wise relative error between a simulated point and a measured point, i.e.,

$$f(p):=\sqrt{ {1\over n} \sum_{k=1}^n \left({s_k(p)-m_k\over m_k}\right)^2}.$$

The variables of the objective function $f(p)$ are shown in Table 14.2. The variables ${\mathrm{d0}}$ and ${\mathrm{dE}}$ determine the diffusivity ${\mathrm{d0}}\cdot{\mathrm{e}}^{-{\mathrm{dE}}/kT}$ of interstitials in silicon.

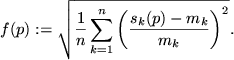
In order to reduce the time needed for the inverse modeling task, the optimization framework SIESTA was used. Its main tasks are optimizing a given objective function and parallelizing the executions of the objective function which usually entails calling simulation tools in a loosely connected cluster of workstations. SIESTA provides several local and global optimizers, the ability to define complicated objective functions, and finally an interface to MATHEMATICA for examining the results. Figure 9.1 shows an overview.

The optimization approach was to first identify reasonable ranges for the variables with great influence, namely energies and exponents. While identifying these ranges suitable starting points for local optimization were found as well. Using these ranges and starting points the optimizations proceeded automatically including all variables.

It was soon found that changing ${\mathrm{cf}}$ and ${\mathrm{cr}}$ did not yield improvements and whenever these variables could be used by a local optimizer, values very close to $1$ resulted. The results described in Table 14.3 and Figure 14.2 were obtained for the high parameter set. Similarly we carried out the same computations for the low parameter set, i.e., TSUPREM-4's default values. These results are shown in Table 14.3 and Figure 14.3.