3.3.5.1 Modified Kinchin-Pease Model

Figure 3.11: Number of silicon vacancies and interstitials generated by the primary recoil as a function of the primary recoil energy assuming a displacement energy of 15 eV.

In the Kinchin-Pease model the number of point defects generated by an implanted ion is derived analytically from the energy that is transfered from an ion to an atom of the target material. It is assumed that the number of point defects generated by a primary recoil is proportional to the energy transfered from the ion to the primary recoil. A primary recoil is a recoil generated by the collision of an implanted ion with a target atom, while secondary recoils are generated by recoils.

As already mentioned each primary recoil generates additional recoils and thereby vacancy-interstitial pairs (Frenkel pairs). Norgett et al. [60] proposed a formula to approximately calculate the number of Frenkel pairs $N_d$ generated by a primary knock-on effect based on an expression given by Kinchin and Pease [44].

$$N_d = \LARGE\left\{\begin{array}{cl} \text{\normalsize0} & \text{... ...rmalsize for $E_{\nu} \geq$\ \LARGE$\frac{2\cdot E_d}{0,8}$} \end{array}\right.$$ (3.143)

$E_{\nu}$ is the energy which goes into nuclear collisions.

$$E_{\nu} = \frac{E}{1+k_d\cdot g(\epsilon_d)}$$ (3.144)

$$g(\epsilon_d) = 3,4008\cdot\epsilon_d^{\frac{1}{6}} + 0,40244\cdot\epsilon_d^{\frac{3}{4}} + \epsilon_d$$ (3.145)

$$k_d = 0,1337\cdot\frac{Z^{\frac{2}{3}}}{M^{\frac{1}{2}}}$$ (3.146)

$$\epsilon_d = \frac{a_0}{\sqrt{8}\cdot e^2}\cdot \left(\frac{9\cdo... ...\frac{1}{3}}\cdot Z^{-\frac{7}{3}}\cdot E = 0,0115\cdot Z^{-\frac{7}{3}}\cdot E$$ (3.147)

$Z$ and $M$ are the charge and the mass of the particles involved in the collision cascade and $E_D$ (displacement energy) is the energy required to remove an atom from a lattice position. (3.145) - (3.147) are simplification of the expressions suggested in [60] assuming that just one particle species is involved in the process.

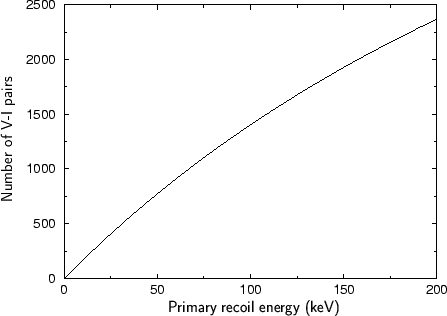
In contrast to the original Kinchin-Pease model this modified model considers also the electronic energy loss of the recoils. Fig. 3.11 show the number of generated vacancies and interstitials as a function of the energy of a primary silicon recoil.

Worth mentioning is that the modified Kinchin-Pease model is valid for energies of the primary recoil below

$$E < 25~keV\cdot Z^{\frac{4}{3}}\cdot M,$$ (3.148)

because the estimation of the energy which goes into electronic stopping is restricted to this regime. But nevertheless this energy limit is approximately 25 MeV for silicon which is significantly higher than the typically ion implantation energy and therefore the highest energy of a primary recoil is also significantly below this limit.

Furthermore this model does not give any information about the location of the vacancies and interstitials. Therefore it has to be assumed that all point defects are located in the vicinity of the position of the primary knock on.