 |
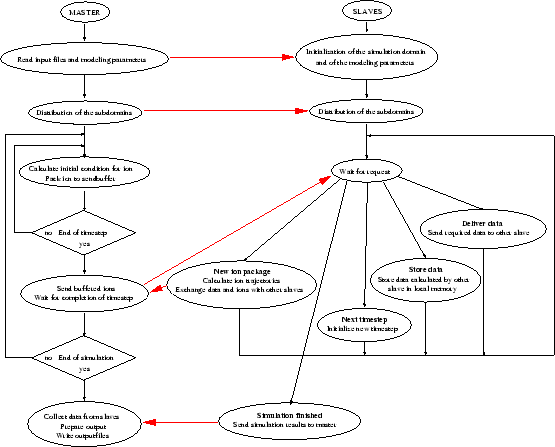
In order to demonstrate the behavior of the parallelization method the complete simulation flow of the master process and of the slave processes is shown in Fig. 4.25.
 |
Master process:
This slightly complicated protocol is necessary to correctly handle
particles that are generated during the simulation either by the trajectory
split method or by the Follow-Each-Recoil method, and to avoid errors due to
communication delays, because the master always knows how many ions were sent to
the network. The Ready Message in common with -1 informs the master that
an additional particle is sent to the network. When all particles within the
network are processed the time step is finished. The performance ![]() of a
slave
of a
slave ![]() is derived from the first Ready Message the master receives from
the slave, by measuring the time interval
is derived from the first Ready Message the master receives from
the slave, by measuring the time interval ![]() between the sending of the
ion package of the first time step and the receiving of the Ready
Message. This is a significant interval because no slave is idle during that
interval.
between the sending of the
ion package of the first time step and the receiving of the Ready
Message. This is a significant interval because no slave is idle during that
interval.
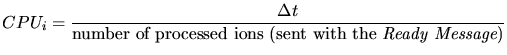 |
(4.15) |
Slave process:
|
The speedup due to parallelization increases almost linear with the number of slaves as could be demonstrated by a three-dimensional simulation on a cluster of identical workstations using one to six slave processes. Fig. 4.27 shows the speedup as a function of the number of slaves. The speedup is determined by the ratio between the simulation time of a parallelized simulation and a simulation with a single slave. The only restriction of the parallelization method is that just slightly varying processor loads are acceptable to achieve a good performance gain.
Worth mentioning is that the Parallelization method is not designed to be failsafe. Whenever one of the slave terminates operation due to a hardware failure the whole simulation ends up in an endless loop. In case of a failure of one slave the master process is not able to determine the end of a time step, because the ions that have to be processed by the terminated slave get lost. This could be avoided by keeping a backup information at the master process and by regularly checking for the operation conditions of the slaves. The implementation of such a mechanism is not recommendable for several reasons.
First the major advantage of the Parallelization method, that the communication overhead due to parallelization is almost negligible, gets lost. If a backup mechanism is implemented not only the initial condition of the ions of one time step have to be stored by the master process, but also the status of the simulation results at the beginning of the time step in order to be able to restart a certain time step in case of a failure of a slave. Since the simulation results are stored locally at the slave all slaves have to send these data to the master process at the end of each time step. In the current implementation of the Parallelization method this is only done at the end of the simulation and nevertheless this is the most communication intensive task during the simulation.
Furthermore a method had to be implemented to replace the failing slave. The most convenient method would be to look for a workstation in the cluster of workstation which does not actually participate in the simulation and to start a new slave process at this workstation. The problem is that the version of MPI which is used for parallelization does not support the spawning of processes during a simulation run. The implementation of such a feature is just announced for future versions of MPI.
An alternative is to redistribute the simulation domain among the remaining slaves, but this requires a huge amount of communication, because all slaves had to be updated with simulation results.
Even if a rigorous implementation of a failsafe mechanism is not recommendable it is probably worth to store the status of the slaves after certain backup intervals and to restart the simulation from such a backup point in case of a failure of one of the slaves. Such a mechanism could be implemented in common with a load balancing mechanism, which anyhow causes an additional communication overhead, because load balancing also requires a redistribution of the simulation domain. The advantage of load balancing would be that strong variation of the loads of the workstation could be compensated and that the performance gain could be increased for the case of strong processor load variations. The biggest challenge for such a parallelization strategy would be to find a clever compromise between the performance gain due to an improved distribution of the simulation domain and the additional communication overhead.
![]()
![]()
![]()
![]() Previous: 4.6.3.2 Optimized Distribution Scheme
Up: 4.6.3 Parallelization Method
Next: 5. Applications
Previous: 4.6.3.2 Optimized Distribution Scheme
Up: 4.6.3 Parallelization Method
Next: 5. Applications