4.4 Model Overview with Coupled Dopant Diffusion

If the advanced oxidation model with its equations for the oxidant diffusion

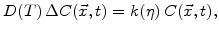$$D(T) \Delta C(\vec{x},t) = k(\eta) C(\vec{x},t),$$ (4.26)

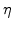
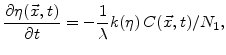dynamics of $\eta$

$$\frac{\partial \eta(\vec{x},t)} {\partial t} = - \frac{1}{\lambda} k(\eta) C(\vec{x},t)/N_1,$$ (4.27)

and mechanical problem

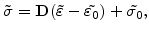$$\tilde{\sigma} = \mathbf{D} (\tilde{\varepsilon} - \tilde{\varepsilon_0}) + \tilde{\sigma_0},$$ (4.28)

is coupled with the five-stream diffusion model for the dopant diffusion, its five continuity equations for the species concentrations

$$\frac{\partial C_{A^+}} {\partial t}=-R_{AI}-R_{AV}+R_{AI+AV}+2R_{AI+AV},$$ (4.29)

$$\frac{\partial C_{I}} {\partial t}=-\nabla J_{I} +R_{AI}-R_{I+V}-R_{AV+I},$$ (4.30)

$$\frac{\partial C_{V}} {\partial t}=-\nabla J_{V} +R_{AV}-R_{I+V}-R_{AI+V},$$ (4.31)

$$\frac{\partial C_{AI}} {\partial t}=-\nabla J_{AI} +R_{AI}-R_{AI+V}-R_{AI+AV},$$ (4.32)

$$\frac{\partial C_{AV}} {\partial t}=-\nabla J_{AV} +R_{AV}-R_{AV+I}-R_{AI+AV}.$$ (4.33)

must be additionally solved.