5.3.1 Thermal Analysis of a Multi-Layered Interconnect Structure

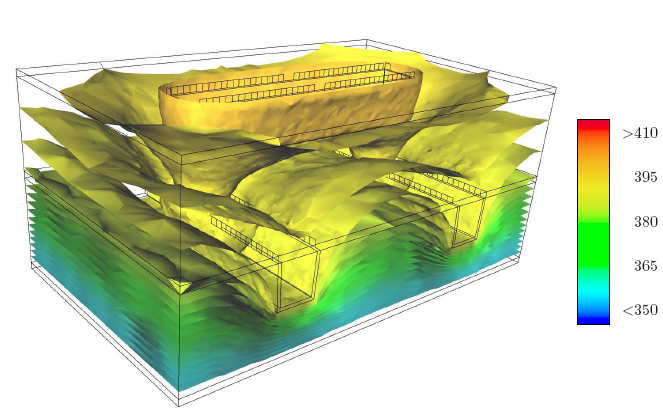
As an example a complex interconnect structures is depicted in Figure 5.18. This particular structure consists of a typical Cu material system with a Ta/TaN coating as presented in Section 2.3, where two Cu lines are connected through a bridge line. These interconnect lines are connected to the each other through Cu vias. The whole structure is embedded in an idealized low- $\kappa$ material with ${{\varepsilon_{\mathrm{r}}}}=3.0$ .

**Figure 5.18:** A bridge between two interconnect lines is biased with a voltage pulse.

Due to the applied bias, the temperature elevates due to self-heating. The resulting temperature distribution in the interconnect lines is shown in Figure 5.19 for 6.6 $\mu$ s and 95.4 $\mu$ s, respectively. As expected, the highest power loss density is located at the bottom of the via structure, which can be seen as the hottest spot in the structure shown in Figure 5.19. Here, the internal temperature distribution of the entire interconnect structure is shown in Figure 5.20. It shows the isothermal surfaces in all materials. The high thermal gradient between the lower Cu lines and the heat sink can be clearly seen by the high density of the isothermal surfaces. At the opposite side -- at the top -- the heat is accumulated and the structure heats up because there is no appropriate thermal path to a heat sink. The maximum temperature is found at the bottom of each via (cf. Figure 5.19). From this location the heat dissipates rather quickly in all directions because the Cu lines provide a good heat conduction path compared to the surrounding low- $\kappa$ material.

**Figure 5.19:** Temperature distribution in a multi-layered interconnect structure at two different points in time showing the global warming in the upper bar that connects the two lower interconnect lines.

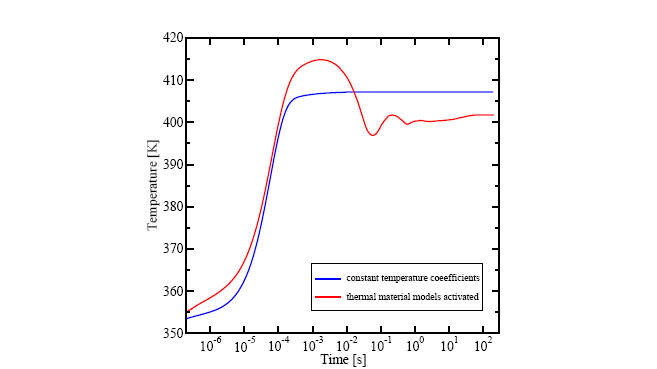
The material models for thermal investigation of complex interconnect structures are often simplified to reduce the computational effort that is necessary to obtain results with in reasonable time. However, if a rigorous transient thermal analysis is required, the difference between simplified models and temperature-dependent models can be significant.

The current examples structure (cf. Figure 5.18) has been investigated once with temperature-independent and then with temperature-dependent material models. The observed difference is depicted in Figure 5.21. While the power loss density is constant for temperature-independent materials, the material properties such as the electrical and the thermal conductivity of temperature-dependent materials changes. In return, this fact affects the power loss density (heat source) and consequently also the temperature. After a certain time, the system reaches a stationary state and the temperature is saturated. However, the value for the stationary temperature is in general different for these types of electro-thermal investigations. For this particular example, the simulation with deactivated thermal material models overestimates the stationary temperature by approximately 5.5 K (cf. Figure 5.21). It should be noted that the transient temperature evolution has a completely different shape due to the dynamic heating behavior of the interconnect stack.

**Figure 5.20:** Temperature distribution [K] in the entire interconnect structure depicted by isothermal surfaces at 95.4 $\mu$ s. The maximum temperature is found at the bottom of each via which is indicated by the isothermal surfaces with the highest temperature and by Figure 5.19.

**Figure 5.21:** The evolution of the maximum temperature in the entire interconnect structure is depicted for activated and deactivated thermal material models.