Next: 2.3.1 Interconnect Materials Up: 2. Thermal Effects in Previous: 2.2.10 Electro-Mechanical Coupling Contents
The bulk properties of materials used in today's Si-based semiconductor devices like conductivities and permittivities are well known. Due to the steady enhancements over the last decades and because the material behavior has changed in terms of purity, doping, and microstructure, the previously well known values of the material properties have to be reconsidered to appropriately account the recently observed discrepancies. However, the values of the bulk properties are still a good approximation of the real values and are thus often used in material models. Once the materials become thinner than a certain threshold size the behavior changes and the material can no longer be considered a macroscopic object. In this case new models have to be applied, which differ from the well known standard bulk models. When the material dimensions are above the threshold value, the new models are required to converge to the well known bulk models.
For anisotropic materials the current density
![]() is proportional to the
electric field
is proportional to the
electric field
![]() by a tensor-valued quantity as
by a tensor-valued quantity as
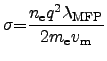 |
(2.122) |
When the layer thickness of the material is reduced to a thin film of only several atomic layers, the electrical conductivity becomes anisotropic. This also happens when grains determine the current flow inside polycrystalline materials. Due to considerable research efforts in material science and in semiconductor process technology [113,31,114,115] most of the materials can be appropriately deposited in such a way that the anisotropic part of the tensors becomes negligible for many applications [116].
To deepen the understanding of the material behavior and to improve reliability, accelerating tests [117,118,119,33] have been introduced, which stress the materials at high temperatures, causing aging effects within a very short time period. This procedure enables life-time tests at the very beginning of the life cycle and at very low costs costs compared to field experiments.