A.1 Convexity of Sets and Domains
A subset
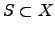 is defined to be convex if for arbitrarily chosen
points
is defined to be convex if for arbitrarily chosen
points 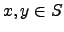 the connection line between these two points
the connection line between these two points
![$\displaystyle [x,y] := (1-\xi) x + \xi y : \xi \in [0,1]\} %\nonumber
$](img890a.png) |
(A.1) |
is completely included in 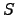 [219,348]. Therefore, the implication
[219,348]. Therefore, the implication
![$\displaystyle x,y \in S \:\:\:\Rightarrow \:\:\:[x,y] \subseteq S$](img892.png) |
(A.2) |
can be applied.
Figure A.1 shows two typical parameter domains. The left domain in this figure
is convex but the second one has obviously not a convex nature.
Figure A.1:
Convexity of domains
 |
For unconstraint parameters of an optimization problem the parameter domain is
convex. If non-linear constraint functions are applied to this problem the parameter space
might be become non-convex. If penalty or barrier functions are used instead
of constraint functions the objective function becomes more complex but the lemmas for
the convergence of these optimization problems can be again applied as for
unconstraint optimization [219,220].
Stefan Holzer
2007-11-19
![]() is defined to be convex if for arbitrarily chosen
points
is defined to be convex if for arbitrarily chosen
points ![]() the connection line between these two points
the connection line between these two points