A.2 VOIGT Notation

The VOIGT notation is used to exploit the symmetry of condensed matter to transform second-order tensors (cf. e.g. stress tensor) to vectors and kinetic forth-order tensors to square matrices (cf. e.g. elasticity tensor) [98]. This notation is often used in continuum mechanics.

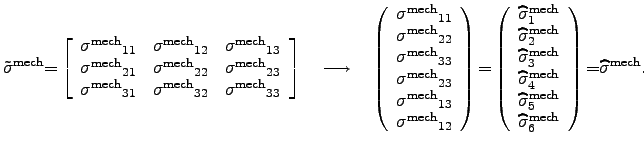
A symmetric tensor, for instance the stress tensor ${\tilde{{\mathbf{{\sigma}}}}^{\mathrm{mech}}}$ in three dimensions, can be written as

$${\tilde{{\mathbf{{\sigma}}}}^{\mathrm{mech}}}{=}\left[ \begin{arr... ...}}_{6}\end{array} \right) {=}{\widehat{{\mathbf{{\sigma}}}} ^ {\mathrm{mech}}}.$$ (A.3)

If the shear components ${\sigma^{\mathrm{mech}}}_{ij}, (i \neq j)$ , can be neglected, the VOIGT transform degenerates to the diagonal operator ${{\mathop\mathrm{diag}}(\cdot)}$ . Hence, the later 3 components of the resulting six-dimensional vector vanish ( ${\sigma^{\mathrm{mech}}}_{ij}=0, i \neq j$ ) and if only orthotropic materials are considered, the shear components always vanish and the six-dimensional vector can be written as a three-dimensional vector.

This simplification can be often applied if only tensile or compressive stress in the direction of one main axis of an orthotropic material is considered.

For the strain tensor ${\tilde{{\mathbf{{\varepsilon}}}}^{\mathrm{mech}}}$ the transformation is very similar. Due to historical conventions, the resulting VOIGT-transform of the strain tensor is the engineering strain ${\mathbf{{e}}}^{\mathrm{mech}}$

$${\tilde{{\mathbf{{e}}}}^{\mathrm{mech}}}{=} \left[ \begin{array}[c]{ccc} {\tilde{e}^{\mathrm{mech}}}_{11} &{\... ...n^{\mathrm{mech}}}_{32} & {\varepsilon^{\mathrm{mech}}}_{33}\end{array} \right]$$

$$\quad\longrightarrow\quad \left( \begin{array}[c]{c} {\varepsilon... ...mech}}}_{6}\end{array} \right) {=}{{\widehat{{\mathbf{{e}}}}}^{\mathrm{mech}}},$$ (A.4)

where ${\tilde{e}^{\mathrm{mech}}}_{\mathrm{ij}}$ , are the components of the engineering strain and the shear strain components transform to the CAUCHY strain components as ${\tilde{e}^{\mathrm{mech}}}_{\mathrm{ij}} {=}2 {\varepsilon^{\mathrm{mech}}}_{\mathrm{ij}}$ , where $i \neq j$ .