Next: 2.2.4 Global versus Local Up: 2.2 Heating Phenomena Previous: 2.2.2 Onsager's Theorem Contents
The local power density is one of the most important quantities that determine the
maximum performance or the maximum number of device operations per time. Moreover,
power has been concentrated at certain local regions
and has therefore to be controlled appropriately to perform the desired action
within the defined requirements.
Unfortunately, power has also a dissipative part. Since the electrical and
mechanical systems have only finite efficiencies, the usable power is less than the
total power consumption.
The difference dissipates via thermal conduction, convection, and radiation. In
addition to that, the second law of thermodynamics postulates the
irreversibility of some of the thermally dissipated heat. Hence, the entropy is
steadily increasing on average.
The appropriate power density for heat conduction can be derived from the local
energy of the electro-magnetic fields,
where the energy of these fields is determined by the POYNTING2.21vector. The spatial power source density of the POYNTING
vector represents the local energy density [58,59], which can be directly derived from
the curl equations of MAXWELL's equations. Multiplying the
equations (2.1) and (2.2) from the left with
![]() and
and
![]() ,
respectively, results in
,
respectively, results in
Equation (2.88) represents the local form of the energy conservation
equation. The left side of (2.88) shows the local source density of the
POYNTING vector which depicts the current change of energy density per time
(power density). The right side shows the different components of the
contribution. The first term
![]() is the electric
component which represents the JOULE power loss that causes self-heating due
to carrier transport2.22mechanisms.
The second and the third term depict the change of the energy stored in the
electrical and the magnetical field, respectively.
is the electric
component which represents the JOULE power loss that causes self-heating due
to carrier transport2.22mechanisms.
The second and the third term depict the change of the energy stored in the
electrical and the magnetical field, respectively.
For isotropic and field-independent materials, (2.88) can be formulated
as
| (2.90) |
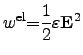 |
(2.91) | ||
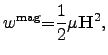 |
(2.92) |
In comparison with common effects in semiconductor devices, JOULE's power loss has often to be taken into account to describe self-heating. In conjunction with semiconductor devices, there are several other approaches to determine the power loss. Since electrons and holes behave differently in semiconductor materials, the current is conveniently split up in order to account for their different properties. In addition, the potential confinement of the carriers is also different. Therefore, the power densities for electrons and holes can be determined with the appropriate models.