2.2.10 Electro-Mechanical Coupling

Transient calculations of electrical or mechanical problems are challenging on their own. If rigorous coupling of these two systems is considered, the effort increases dramatically, e.g, different requirements of mesh generation for critical regions have to be considered for the electrical simulation as well as for the mechanical simulation. In particular, for regions which do not mainly influence the current distribution or the electric field, a coarse mesh can be applied for the electrical analysis in these regions. However, these regions may be critical ones during the mechanical investigation and might thus be essential for the global device characteristics.

Much effort for TCAD analysis is due to the increasing importance of thermal issues in microelectronic device structures. Therefore, the analysis for the electrical and mechanical problems becomes even more challenging because of the complex simulation tasks and the difficulty to couple the sub-systems self-consistently. Also, mechanical and geometrical constraints as well as boundary conditions are influenced by the temperature and raise the grade of complexity. For instance, if the local temperature increases, it forces the materials to expand and thus to increase the local stress or to perform deformations at weak material interfaces.

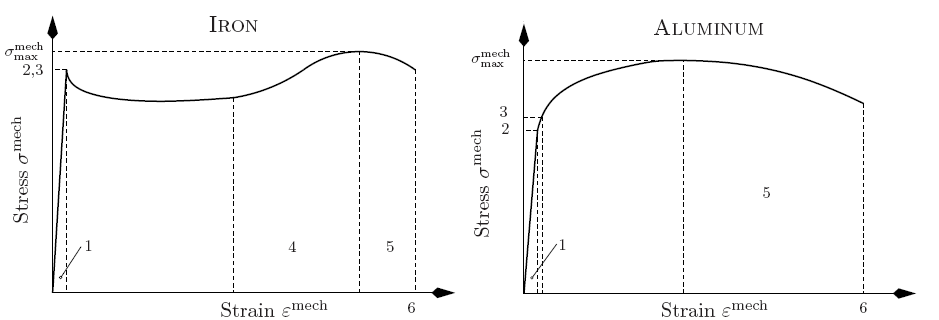
Therefore, viscoelasticity can be assumed as long as the material is in the linear regime because after removing the external stress the materials relaxes until a residual stress level. The remaining stress level is relaxes due to diffusion processes of the atoms in the material. Within this small linear regime, the material parameters change only within a small range. But above this certain threshold value, inelastic deformations occur and also the material parameter might change abruptly, as it is shown in Figure 2.4.

Figure 2.4: Mechanical stress as a function of mechanical strain, showing different regimes of behavior
for the ductile materials iron ( ${\mathrm{Fe}}$ ) and aluminum ( ${\mathrm{Al}}$ ). The Following distinctive points can be
determined for different materials: $\sigma_{\mathrm{max}}$  ultimate strength, 1. linear regime, 2. yield strength
3. proportional limit for stress 4. strain hardening region 5. necking region 6. rupture point

The materials used in microelectronics show worse characteristics than bulk materials because the thicknesses are in the range of tens of nanometers, where the microscopic grain structures as well as material interfaces drastically influence the material parameters.

In Figure 2.4 the mechanical strain-stress curves of two typical materials are presented, where the normal operation conditions are typically located in the low linear regions. When the temperature increases, the volume expands and additional strain ${\varepsilon^{\mathrm{mech}}}$ and therefore, stress ${\sigma^{\mathrm{mech}}}$ occurs and the bias point is shifted from the original linear region towards higher strain values. The maximum stress level for a linear strain-stress relation is marked by point 3 in Figure 2.4 for ${\mathrm{Fe}}$ and ${\mathrm{Al}}$ . For ${\mathrm{Fe}}$ point 2 and 3 coincide. A quite a good linear approximation for the stress characteristics can be applied as long as the stress level is below the ``yield strength'' (marked as point 3). Above this yield strength point, the stress characteristics show a highly non-linear behavior. For most metals and some other materials the elastic limit and the yield strength are essentially the same [110,111]. Hence, beyond this point plastic deformations occur due to reordering of the grains and the crystal structure can be observed. Further increase of strain pushes the stress towards its maximum at ${\sigma^{\mathrm{mech}}}_{\mathrm{max}}$ . After the maximum stress level has been reached, further strain enhancement causes material necking until the material ruptures.

Figure 2.5: Schematic overview of the self-consistent electro-thermo-mechanical simulation tool flow.

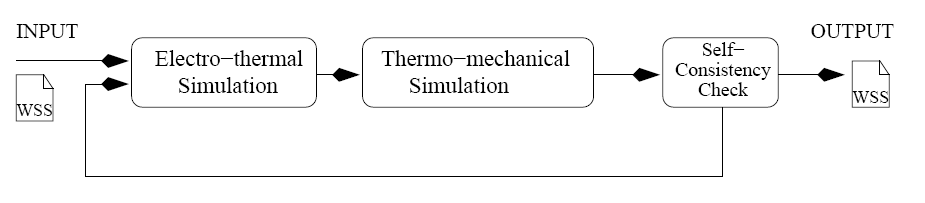To see the impact of increasing temperature within mechanical simulations, both the electro-thermal and the thermo-mechanical equation system have to be solved for each time step. Because of different requirements for the simulation of electrical and mechanical problems, a combined simulation within a single simulator requires a lot of memory which often exceeds the physically available amount in high-end simulation nodes. Therefore, the simulations have been separated to a self-consistent simulation flow, as shown in Figure 2.5. This self-consistent approach for solving electro-thermal and thermo-mechanical problems provides as benefits that already existing simulation tools with well-established and calibrated simulation models can be used, and in addition to that these simulators are already optimized and well-tuned for their specific problems. As a drawback, since this approach is an iterative one, cutting down to subproblems results in longer execution time because for each iteration the complete loop has to be carried out until a stationary state has been reached.

To shorten the simulation time to the absolute necessary, an additional ``self-consistency check'' has been introduced which checks the update of the simulation result (cf. Figure 2.5). For very small updates of the temperature or the constraints due to mechanical changes, the simulations results will not be affected too much. Hence, the error if the consistency loop is not closed is negligible. However, as an additional safety measure, the self-consistency loop can be closed at certain user-defined check points.