2.3.1.1 Metals and Silicides

To improve the transistor switching characteristics high current densities have to be provided by interconnect lines. Because the dimensions of the interconnect lines cannot be increased as required, the performance becomes limited by signal delays due to the transistor transfer characteristics as well as by signal delays due to the parasitic resistances, capacitances, and inductances.

One of the requirements for shrinking a technology is that the voltage and the current remain at the same order of magnitude in order to provide backward compatibility to former circuit designs. But when the current remains constant at shrinking device feature sizes the current density increases quadratically with feature size reduction.

In order to provide good conduction properties for good device characteristics, a low sheet resistivity of the interconnect lines is not sufficient. Moreover, a low contact resistivity to other parts of the device, e.g. to bonding wires, vias, and semiconductor regions, is required. The phase state of conducting materials has to be mechanically stable over a wide temperature range, which also implies that the diffusion of ions into adjacent material regions has to be negligible. This requirement is very important for narrow interconnect lines, where the diffusion of some metals provide additional trap sites in the dielectrics and additional dopants in semiconductor materials, which would result in a long-term change in the device characteristics. One of these effects is called ``contamination''. It reduces reliability and lowers the quality of the device characteristics. The second effect is called ``poisoning'', which not only reduces but can destroy the device characteristics immediately due to changes in the doping profile. However, both effects destroy the desired device characteristics if a longer period of time is considered.

To provide appropriate barrier and protective layers the compatibility of the materials has to be clarified according to the requirements of the device structures to avoid performance reductions due to mechanical and electrical material constraints. This can be done for instance by matching volume expansion coefficients. Furthermore, another serious concern related to the introduction of new materials into an existing process is the cost of ownership (COO). Since certain materials require special treatments in terms of safety for the device structures, the fabrication equipments and the environmental laws, additional costs have to be considered as well in advance. However, if there are more benefits than costs, the materials are introduced to the semiconductor device structure if the following requirements can be fulfilled [127]:

• The new materials have to avoid unintentional reactions with other materials, for instance with dielectrics or semiconductors in order to provide a stable material stack during device operation.
• High process yield is required to minimize the material-induced and process-related fabrication failures.
• Grain engineering allows the designers to modify and adjust the statistical distribution of the grain shapes and structures.
• It is important that the material can be easily patterned, which offers cheap and fast technology processes to deposit and etch the material.
• The new materials have to be stable in oxidizing chemical environments and oxidizable at certain defined ambient conditions to provide well-controlled material patterning processes.
• A good adherence is mandatory to avoid unintentional material dissolutions.
• Low residual stress levels from fabrication processes are desirable to allow mechanical relaxation of surrounding materials for a mechanically stable material stack.
• Smooth surfaces and interfaces to other materials are required to obtain well-defined interface conditions and low impurity concentrations at material interfaces for increased reliability.
• A rather long life-time of the material stack is required to meet the reliability requirements given by the device specifications.

For silicides (salicides) additional requirements apply [127]:

• The material has to remain stable throughout processing to avoid diffusion into other materials as well as to preserve the stoichiometric material compositions.
• Minimal reactions with metalization layers, e.g.  ${\mathrm{Al}}$ , ${\mathrm{W}}$ , ${\mathrm{Cu}}$ , ${\mathrm{Ta}}$ , and ${\mathrm{Ti}}$ to provide stable material stacks and to offer stable diffusion barrier layers for certain metals is necessary.
• Minimal junction penetration to offer good contacts due to the ${\mathrm{Si}}$ consumption. A low ${\mathrm{Si}}$ consumption is required to preserve a proper operation in ${\mathrm{Si}}$ region and in the semiconductor junctions.

${\mathrm{Al}}$ has served very well for several decades as an interconnecting material and for bonding pads. Al shows a high conductivity but has the disadvantage that it generates a native oxide ( ${\mathrm{Al_2O_3}}$ ), which is very stable, similar to $\mathrm{SiO_2}$ . However, ${\mathrm{Al_2O_3}}$ is thermally and chemically much more resistant than $\mathrm{SiO_2}$ . Therefore, preventing oxidation of ${\mathrm{Al}}$ is very important during the fabrication process. Yet, even though the process is very well controlled, the higher demands related to higher current densities, brought up the problem of electro-migration, which has forced several companies to changes the interconnect base material to ${\mathrm{Cu}}$ . Bulk ${\mathrm{Cu}}$ has a much lower tendency of electro-migration than ${\mathrm{Al}}$ . On the other hand, the ${\mathrm{Cu}}$ integration into the technology nodes requires more effort due to the higher diffusivities and solubility of ${\mathrm{Cu}}$ into the standard materials used in the interconnect stack. To prevent the diffusion of ${\mathrm{Cu}}$ into ${\mathrm{Si}}$ , $\mathrm{SiO_2}$ , and other materials, additional coating and barrier layers have to be introduced. However, the introduction of such barrier layers posed new challenging effects that had to be overcome. The adhesion of copper on typical barrier layers is very weak, which results in high-diffusive paths at material interfaces with ${\mathrm{Cu}}$ . Hence, these weak interfaces reduce the activation energy for ion diffusion significantly, increasing the electro-migration effects and thereby decreasing the reliability of ${\mathrm{Cu}}$ -based technology. Due to new materials for barrier layers at material interfaces to ${\mathrm{Cu}}$ , the reliability of ${\mathrm{Cu}}$ interconnects can be better controlled within a certain range to meet the circuit design requirements.

Therefore, the interconnects have protective layers around the ${\mathrm{Cu}}$ . In addition to this measure, the lowest layer contacting the ${\mathrm{Si}}$ surface is still made of ${\mathrm{W}}$ , as known from the ${\mathrm{Al}}$ technology. The reason for that - once again - is reliability. If ${\mathrm{Cu}}$ diffused into the dielectric in a higher interconnect stack level, the ${\mathrm{Cu}}$ could contaminate and thereby reduce the dielectric reliability in terms of resistivity, break through voltage, and other parasitics: Nevertheless, the device structure would still be functional. If, e.g., ${\mathrm{Cu}}$ atoms diffused into the ${\mathrm{Si}}$ regions, a significant shift of the threshold voltage is observed. As a result, the transistor would no longer be working properly resulting in complete device failure. Hence, to ensure that ${\mathrm{Cu}}$ atoms cannot contaminate the ${\mathrm{Si}}$ regions, the lowest via level is made of a less contaminating material than ${\mathrm{Cu}}$ .

Figure 2.8: Tungsten via containing several materials as diffusion barriers.

Figure 2.8 shows a typical via made of ${\mathrm{W}}$ and ${\mathrm{Ti}}$ compounds as used in standard ${\mathrm{Al}}$ technology nodes, and as first-level vias in ${\mathrm{Cu}}$ technology nodes. For this structure it is important to note that the contact to the semiconductor consists of ${\mathrm{TiSi_2}}$ . On top of the ${\mathrm{TiSi_2}}$ contact layer is a Ti layer, which comes from the fabrication process in which Ti is deposited on top of the Si substrate. The ${\mathrm{TiSi_2}}$ layer is formed either by diffusion,

$$\mathrm{2 Si + Ti {\quad\stackrel{\! }{\rightarrow}}\quad TiSi_2},$$ (2.127)

or by explicit ${\mathrm{TiSi_2}}$ deposition, following [127]

$$\mathrm{TiCl_4 + 2 SiH_4 + Si} {\quad\stackrel{\! }{\rightarrow}}\quad \mathrm{{{\mathrm{TiSi_2}}} + SiClH_3 + 3HCl + H_2},$$ (2.128)

$$\mathrm{TiCl_4 + H_2} {\quad\stackrel{\! }{\rightarrow}}\quad \mathrm{TiCl_2 + 2 HCl},$$ (2.129)

where (2.128) shows a reaction in which also a consumption of solid ${\mathrm{Si}}$ occurs. By applying the appropriate temperature and optimal HCl concentration, the ${\mathrm{Si}}$ consumption can be avoided according to [127] by

$$\mathrm{TiCl_4 + 3 SiH_4} {\quad\stackrel{\! }{\rightarrow}}\quad \mathrm{{{\mathrm{TiSi_2}}} + SiClH_3 + 3HCl + 3H_2}.$$ (2.130)

However, this reaction is only stable for a certain chemical environment and certain temperatures. The chemical reaction can be further controlled by adjustments of the concentrations of silane (SiH$_4$ ) and hydrogen:

$$\mathrm{TiCl_4 + 2 SiH_4} {\quad\stackrel{\! }{\rightarrow}}\quad \mathrm{{\mathrm{TiSi_2}}+ 4HCl +2H_2}$$ (2.131)

$$\mathrm{Si + 2 HCl} {\quad\stackrel{\! }{\rightarrow}}\quad \mathrm{SiCl_2 +H_2}.$$ (2.132)

In this reaction, the ${\mathrm{Si}}$ consumption underneath the ${\mathrm{TiSi_2}}$ layer can be controlled by the concentration of silane, which is quite stable at a typical processing temperature of 800$^{\circ}$ C and a pressure of approximately 250Pa (2Torr).

On top of the ${\mathrm{TiSi_2}}$ layer, a thin ${\mathrm{Ti}}$ layer is deposited that is covered by a ${\mathrm{TiN}}$ film. The ${\mathrm{TiN}}$ serves as a diffusion barrier for the ${\mathrm{W}}$ via. In optical stacks, ${\mathrm{TiW}}$ can be used instead of ${\mathrm{TiN}}$ to reduce reflections of light at interfaces.

For the ${\mathrm{Cu}}$ technology nodes, requires additional protection is required, since the size of the ${\mathrm{Cu}}$ atoms is smaller than that of ${\mathrm{W}}$ . Furthermore, ${\mathrm{Cu}}$ shows a higher tendency to diffuse into the dielectrics. The first attempt was the application of thicker layers of ${\mathrm{TiN}}$ , but at the early stages of ${\mathrm{Cu}}$ technologies, the adhesion of ${\mathrm{Cu}}$ metal to ${\mathrm{TiN}}$ was much weaker than expected [128]. With down-scaling and increasing current densities, the weak material interface caused too many failures, and so alternative material compounds were investigated. As a logical consequence, ${\mathrm{TiN}}$ was replaced by other nitrates. The most suitable of them ( ${\mathrm{TaN}}$ ) improved interface adhesion, but was not quite satisfactory. Hence, an additional ${\mathrm{Ta}}$ layer has been introduced to the ${\mathrm{Cu}}$ technology node, providing a sealing film over the ${\mathrm{Cu}}$ interconnect structures. Between ${\mathrm{Cu}}$ and ${\mathrm{TaN}}$ , an alloy of ( ${\mathrm{Ta}}$ ${\mathrm{Cu}}$ ) [33] -- due to the high-temperature phase during the fabrication, in which both materials diffuse into each other -- builds up. Recent arrangements have been proposed where the sealing ${\mathrm{TaN}}$ layer is replaced by a ${\mathrm{Ta}}$ layer only. Compared to the high resistivity of ${\mathrm{TiN}}$ , the ${\mathrm{Ta}}$ layer provides the advantage of much higher conductivity. Hence, the ${\mathrm{Ta}}$ layer offers an additional conductive path, which becomes importance for further down-scaling in interconnect structures. The lower limit of the thickness of the ${\mathrm{Ta}}$ layer, however, is approached. Hence, the resistance increase in smaller interconnects is still considerable, calling for research into alternative materials suitable for the future technology nodes.

A new approach has been reported which uses ${\mathrm{Mn}}$ as barrier layer for ${\mathrm{Cu}}$ interconnects [129,130]. In this case, as interconnect material ${\mathrm{Cu}}$ ${\mathrm{Mn}}$ alloy is deposited. With increasing temperatures, the ${\mathrm{Cu}}$ grains reach their final size and shape, and the ${\mathrm{Mn}}$ impurities accrete at material interfaces, but mostly at the interconnect surface. Due to diffusion and accretion processes of ${\mathrm{Mn}}$ impurities, the resulting thickness of the ${\mathrm{Mn}}$ barrier layer is in the range of a few atomic layers (12 to 40 Å). Hence, this procedure offers a good alternative to the previously used ${\mathrm{Cu}}$ ${\mathrm{Ta}}$ solutions, where the thickness of the thin ${\mathrm{Ta}}$ layer is limited to 25 to 50 Å with relatively a high standard variations, compared to the ${\mathrm{Ta}}$ layer thickness.

The ${\mathrm{Al}}$ and the ${\mathrm{Cu}}$ technology use ${\mathrm{Si_3N_4}}$ as etch-stop layer, where the mechanical properties, especially the hardness of ${\mathrm{Si_3N_4}}$ , forced the technology developers to find better materials. In particular, a material was sought more suitable for chemical-mechanical polishing (CMP) than $\mathrm{SiO_2}$ . Because of the extreme hardness of ${\mathrm{SiC}}$ , this material is well fitting to these needs but the manufacturing process is very difficult. On the other hand, as experiments have shown, $\mathrm{SiO_2}$ is still a good alternative, and now used as top layer in the interlayer dielectrics (ILD) stack even though it originally had been substituted by other alternative materials. The use of these new materials introduced too many problems and challenges during the CMP process so that a return to the original material was indicated. With $\mathrm{SiO_2}$ as top ILD layer, the original technique for CMP can be applied and the well known effects such as dishing can be considered by the same design rules as before.

Figure 2.9: Thermal conductivity and specific heat capacitance of various common interconnect materials compared to Si and Ge. [131,132,133,134,135,136,137,138]

The requirements for the use of metals in interconnect structures can be summarized as follows:

• A high electrical conductivity is mandatory to minimize the power loss due to high electrical loads carried by the interconnect lines, especially for thin shallow structures such as vias in the lower metalization levels.
• A high thermal conductivity is desired to provide heat conduction paths with low heating due to the heat transport and to control the heat flow through the whole semiconductor device from the heat sources to the heat sinks.
• The microstructure of the metal should be controllable within a certain range to reduce the scattering effects in order to facilitate a more precise estimate of the thermal impact of this effect, which then can be considered in the design process.
• Thermal stability over a wide range is also a very important feature that offers on the one hand a stable material during fabrication, and a reduced diffusivity into other materials, and on the other hand a mechanical rigid solid. However, this property is not available from just any material. For instance, ${\mathrm{B}}$ and ${\mathrm{Cu}}$ atoms show high diffusivities in many materials, especially into dielectrics and semiconductors.

Table 2.1: Characteristic electrical parameters of typical materials used interconnect structures and contacts.

Material	$\sigma_0$	$\alpha_{\sigma}$	References
$\mathrm{T}=300\mathrm{K}$	$[1/{\mu\Omega\mathrm{cm}}]$	$[10^{-3}\mathrm{K}^{-1}]$
Ag	$0.613-0.629$	$4.1$	[139,140]
Cu	$0.588-0.645$	$3.65-6.8$	[141,33,139,142,4,140]
Au	$0.425-0.49$	$4.0$	[139,142,140]
Al	$0.33-0.4$	$4.3-5.0$	[142,39,140]
W	$0.2$	$-$	[142]
Ta	$0.057-0.072$	$-$	[142,33]
Ti	$0.012$	$-$	[142]
TiSi$_2$	$0.0625-0.0769$	$-$	[143,144,127]
WSi$_x$	$0.0125-0.0333$	$8.9$	[143,127,47]
TaSi$_2$	$0.0182-0.0285$	$-$	[143,127]
TiN	$0.0167-0.025$	$4.1$	[127,39]

Tab. 2.1 presents parameters for the electrical conductivity for materials which are commonly used in interconnect structures. Compared to Tab. 2.1, Figure 2.9 shows a comparison of thermal conductivities of common interconnect materials, set into relation with the semiconductor materials Si and Ge. As can be directly seen from Figure 2.9, the thermal conductivity of metals depend only slightly on temperature. With rising temperature the semiconductors ${\mathrm{Si}}$ and ${\mathrm{Ge}}$ show a marked decrease of thermal conductivity. This effect can be explained by the main heat transport mechanism in metals and metal-like materials such as semiconductors. At low temperatures, the electron gas in metals has a certain average energy and -- with a certain bias applied -- the electron gas transports the information such as electrical current or heat with very little loss to the opposite side. Hence, the electrical and the thermal conductivity can be modeled by the WIEDEMANN^2.34-FRANZ^2.35-LORENZ^2.36 law, where the ratio between the electrical and the thermal conductivity is proportional to the absolute temperature. Conducting materials with a perfect lattice have no resistance, hence infinite electrical conductivity [142]. According to the WIEDEMANN-FRANZ-LORENZ law, also the thermal conductivity would be infinite. However, the crystals are not perfectly periodic and the crystal planes are also not perfectly aligned. Therefore, the electrons are scattered and, as temperature increases, also scattering increases due to several additional effects.

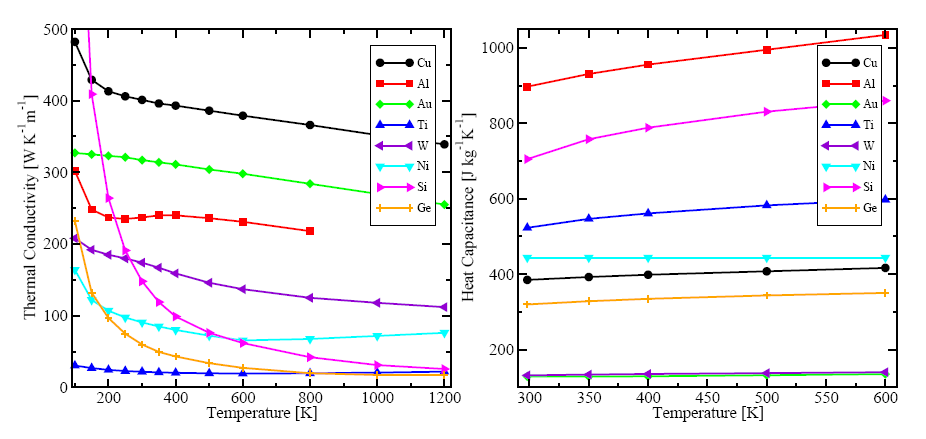
The according specific heat capacitances are presented in Figure 2.9, which shows that the tendency of the semiconductors and the different metals from Figure 2.9 is quite the similar.

However, a rigorous electro-thermal analysis, especially in the high frequency domain, has to include electro-magnetic effects like the skin effect, which reduces the conductivity due to a limited electro-magnetic field penetration into the metal [145,146,147]. The penetration depth ${d}$ is expressed as

$${d}{=}\sqrt{{2}\over{\omega \sigma \mu} },$$ (2.133)

where $\omega$ is the angular frequency, $\sigma$ the electrical conductivity, and $\mu$ the magnetical permeability. As a consequence the resulting local current density $J({\mathbf{{x}}})$ can be approximated with the analytical solution for a cylindrical solid [59]

$$J({\mathbf{{x}}}) {=}J_0 \exp\left(-\frac{\vert{\mathbf{{x}}}-{\mathbf{{x}}}_{\mathrm{Surface}}\vert}{{d}}\right),$$ (2.134)

where $J_0$ is the DC current density and ${\mathbf{{x}}}_{\mathrm{Surface}}$ is the closest point of the surface of the conductor. The temperature dependence in (2.133) and (2.134) is implicitly present and determined by the well known temperature dependencies of the materials parameters used.