2.3.1 Interconnect Materials

The performance of digital semiconductor devices is determined by two issues: the switching behavior of the semiconductor itself and the signal delays due to the interconnects, which include metal lines, vias, the necessary protective coatings, barrier layers, and parasitic capacitances. Both parts are of the same order of magnitude whereby the contribution of the interconnect lines has gained more significance at every new technology node [10,3].

Shrinking the technology node affects at first the transistor gate lengths and the area of the transistors, but also its surrounding elements such as contacts, vias, and interconnect structures. Since the dimensions of the interconnects have to be scaled down accordingly, the small additional protective coatings, barrier layers, and vias become more and more important [5,120]. For instance, if a metal line with a rectangular-shaped cross-section of one square micrometer is considered, a $25\mathrm{nm}$ thick coating reduces the active metal cross-section by $5\%$ . If the interconnect line is scaled down to $90\mathrm{nm}$ , the coating thickness cannot be reduced that much. Hence a minimum thickness of approximately $5$ to $10\mathrm{nm}$ still remains. This geometry would result in a reduction of the active cross-section by 11 to $21\%$ , respectively.

However, the cross-sections of the conductive materials are only one of several factors for the increasing resistivity. As Figure 2.6 shows, scaling down the dimensions for interconnects according to the ITRS [3,121] results in a considerable increase of the interconnect resistivity.

Figure 2.6: Relative resistancy increase for copper as a function of line width [3].

The different contributions for lowering the conductivity as a function of the interconnect line dimensions are also shown. The figure shows the two main phenomena for the increase of the line resistance: The dominant factor is the reduction of the mean free path of the charge carriers, which can be observed by increased surface scattering due to line narrowing. A second important factor is the internal microstructure of the material, which can be described with a grain boundary model (cf. Section 2.3.2).

The following part of this section deals with the resistance increase due to the confinement of the trajectories of the electrons. The reason for the confinement of the trajectories of the electrons in metal lines is the internal microstructure (grains) and the fact that the macroscopic geometry of the metal lines comes into the range of the dimensions of the microstructure of the material. Both the grain boundaries and the surfaces of the solids are barriers for the charge carriers. Moreover, at barriers and surfaces the crystal structure is distorted and the impurity concentration is rather high compared to the bulk material. Therefore, the charge carriers scatter also at these impurity sites.

Figure 2.7: Resistance raise due to increased scattering events resulting from line narrowing of interconnect path dimensions.

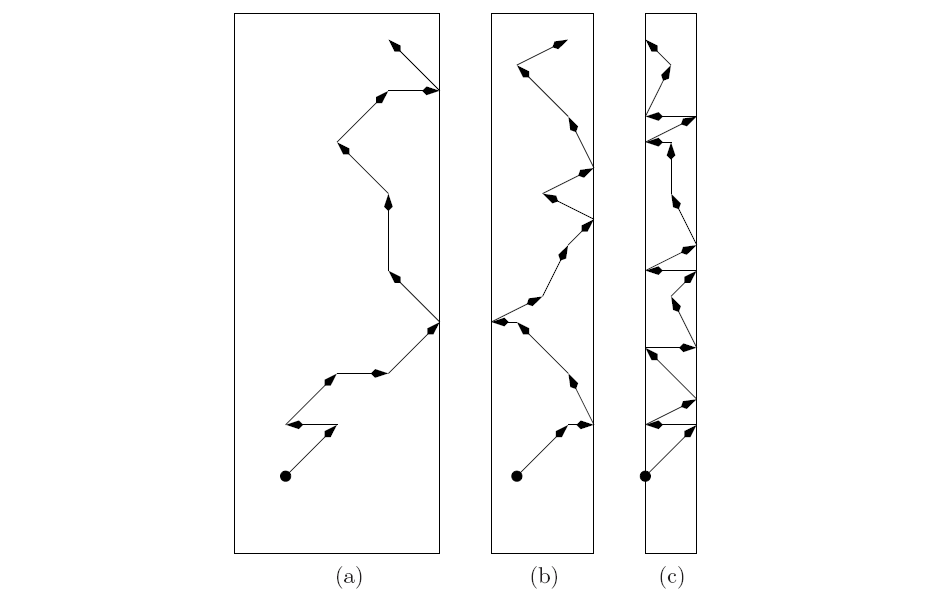Since the deposition process cannot be guaranteed to result in a single crystalline material, it has to be considered polycrystalline. Due to the advances in process technology, especially for metal lines, the type and the shape of the distribution of grains can be controlled in wide ranges. However, the presence of grains cannot be avoided, but their shape can be adjusted appropriately, at least for certain metals. With this technology enhancement, many former serious problems can be simply avoided or minimized. Hence, the impact of the polycrystalline behavior can often be neglected, for instance if the number of grain boundaries is small or when current flow is perpendicular to the average grain boundary surface. Therefore, metals can be mostly considered as single-crystalline solids which simplifies the numerical investigation of transient electro-thermal problems enormously.

The part of the resistivity that results from the grain structure can be reduced to a certain minimum. However, the geometry introduces absolute physical constraints according to the maximum resistance allowed and the expected current load for the interconnects. These requirements are given by the technology node and the design rules and cannot be changed. Thus, a resistance increase due to increased surface scattering events has to be taken into account from the beginning of the design stage. As Figure 2.6 shows, the bulk resistivity of some metals (e.g. copper) is only valid for thick metal lines. For thin wires, a significant resistance increase is observed, which has to be considered during the design phase of the integrated circuit.

To determine the difference between the resistance of a bulk material and the resistance of the same material as a thin film, the scattering effects have to be considered according to the narrowing effect.

For a one-dimensional resistivity increase due to confinement of charge carriers, for instance in a flat parallel-sided slab, FUCHS^2.33 [122] derived the expression

$$\frac{\rho_0}{\rho} {=}1 - \frac{3}{2} \frac{1-{p_{\mathrm{sc}}}}... ...\kappa x\right)}}{1-{p_{\mathrm{sc}}}\exp{\left(-\kappa x\right)}} \mathrm{d}x,$$ (2.123)

where

$$\kappa {=}\frac{d_{\mathrm{min}}}{{\lambda_{\mathrm{MFP}}}}$$ (2.124)

represents the ratio between the smallest distance in the thin film $d_{\mathrm{min}}$ and the mean free path of the charge carriers ${\lambda_{\mathrm{MFP}}}$ and the fraction of charge carriers that elastically scatter at the material surface is denoted by ${p_{\mathrm{sc}}}\in [0,1]$ . The mean free path of electrons in bulk ${\mathrm{Cu}}$ has been reported to be in the range of $39\mathrm{nm}$  [121,123,124] to $41.2\mathrm{nm}$  [5] in a temperature range of $300\mathrm{K}$ and $273.15\mathrm{K}$ . 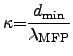The mean free path for electrons in bulk ${\mathrm{Al}}$ is much shorter, for instance $14.8\mathrm{nm}$ at room temperature [124].

For thick material layers as well as for thin film layers (compared to the length of the mean free path), (2.123) can be simplified according to [125,126] as

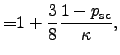$$\frac{\rho_0}{\rho} {=}1 + \frac{3}{8}\; \frac{1-{p_{\mathrm{sc}}}}{\kappa} , \kappa \gg 1,$$ (2.125)

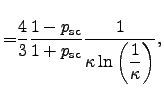$$\frac{\rho_0}{\rho} {=}\frac{4}{3}\; \frac{1-{p_{\mathrm{sc}}}}{1+{p_{\mathrm{sc}}}} \frac{1}{\kappa \ln{\left(\displaystyle{\frac{1}{\kappa}}\right)}} , \kappa \ll 1.$$ (2.126)

The approximation for $\kappa \gg 1$ is still used for interconnect materials because the technology nodes still operate at feature sizes with $\kappa \geq 1$ .

However, to facilitate further down-scaling parasitic effects have to be reduced by optimizing the materials in terms of geometry and purification. For instance impurities aggregate at grain boundaries and material interfaces. Hence, device fabrication becomes more and more expensive due to the requirements of highly pure materials used in the device structures. Further enhancements of process technology nodes are very costly and require the consideration of new materials to improve the device characteristics as well as to reduce the fabrication costs. For instance, silicided metals are a good alternative for gate contacts and for barrier materials to protect silicon. This type of material compound is very common in today's semiconductor devices.