Next: 2.3.1.4 Barrier Layers Up: 2.3.1 Interconnect Materials Previous: 2.3.1.2 Semiconductors as Conducting Contents
Non-conducting, insulating materials are called dielectrics and
provide a band gap
![]() which is typically larger than 4 eV.
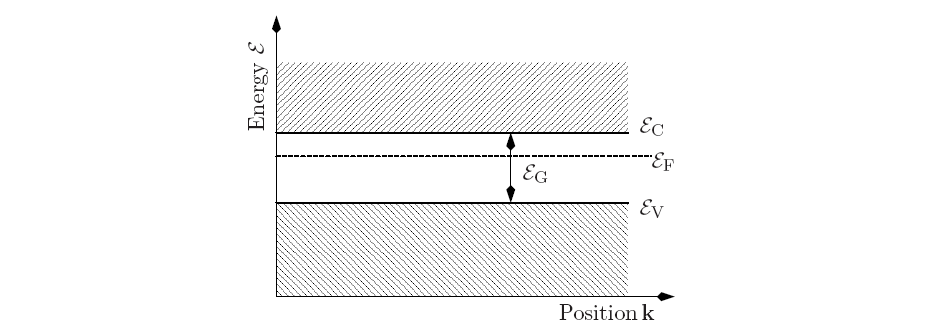
Figure 2.10 shows a typical band edge diagram for a semiconducting material.
Here, the energy levels
which is typically larger than 4 eV.
Figure 2.10 shows a typical band edge diagram for a semiconducting material.
Here, the energy levels
![]() ,
,
![]() ,
and
,
and
![]() are the conduction band energy, the valance band
energy, and the FERMI level, respectively. The FERMI level is
defined as the energy for which the occupation probability is exactly
are the conduction band energy, the valance band
energy, and the FERMI level, respectively. The FERMI level is
defined as the energy for which the occupation probability is exactly
![]() .
The activation of an electron from the valence band to the conduction band
requires the energy of the band gap. This type of energy can be either of
potential, kinetic, or thermodynamic nature.
.
The activation of an electron from the valence band to the conduction band
requires the energy of the band gap. This type of energy can be either of
potential, kinetic, or thermodynamic nature.
 |
Natural quantities to describe dielectrics are the conductivity
![]() , the band gab
, the band gab
![]() , the relative dielectric constant
, the relative dielectric constant
![]() ,
the break-down voltage, and the melting, respectively the boiling point for
fluid dielectrics.
For modern semiconductor devices, the conductivity and the break-down
voltage have lost importance because the design can control the internal
voltage distribution very well and the conductivity of the insulating material
are considered together with their leakage behavior including tunneling effects
in gate dielectrics.
,
the break-down voltage, and the melting, respectively the boiling point for
fluid dielectrics.
For modern semiconductor devices, the conductivity and the break-down
voltage have lost importance because the design can control the internal
voltage distribution very well and the conductivity of the insulating material
are considered together with their leakage behavior including tunneling effects
in gate dielectrics.
For thicker dielectric layers, the capacitances are more important than the conductivities because the impact of cross talk between different interconnect lines is mainly determined by the capacitive coupling. This phenomenon can be investigated only if the final chip layout has been designed.
The relative dielectric constant
![]() is the most important quantity in
microelectronics to characterize the insulation material since the capacitive
coupling of two structures should be either ideally if the current flow has to be
controlled, e.g. in a transistor or has to be avoided to reduced cross talk
between interconnect structures.
However, the constant has certain limits in both directions: If no matter is
present the relative dielectric constant has its lower bound with
is the most important quantity in
microelectronics to characterize the insulation material since the capacitive
coupling of two structures should be either ideally if the current flow has to be
controlled, e.g. in a transistor or has to be avoided to reduced cross talk
between interconnect structures.
However, the constant has certain limits in both directions: If no matter is
present the relative dielectric constant has its lower bound with
![]() .
The upper bound is given by the crystal structure of the material.
Some materials, such as Perovskites and PZTs [140], provide extremely
high relative dielectric constants. As a drawback, these materials often show a
quite low stability in terms of the repolarisation and temperature.
However, in certain applications these materials can be applied as well.
.
The upper bound is given by the crystal structure of the material.
Some materials, such as Perovskites and PZTs [140], provide extremely
high relative dielectric constants. As a drawback, these materials often show a
quite low stability in terms of the repolarisation and temperature.
However, in certain applications these materials can be applied as well.
![]() has been used in a wide range of applications because it is easy and
cheap to produce and is rather stable in electrical and thermal terms, and very
chemically resistant.
Therefore,
has been used in a wide range of applications because it is easy and
cheap to produce and is rather stable in electrical and thermal terms, and very
chemically resistant.
Therefore,
![]() is very often used for instance as insulation material in
control gates in transistors where a rather high dielectric constants would be
required.
But due to the low costs and simpleness of the fabrication of
is very often used for instance as insulation material in
control gates in transistors where a rather high dielectric constants would be
required.
But due to the low costs and simpleness of the fabrication of
![]() , this
material is still used as gate dielectrics and as passivation
and insulation layers in interconnect structures to encapsulate the
interconnecting lines from each other. In the latter example, a very low
dielectric constant is the optimum for the overall device performance.
, this
material is still used as gate dielectrics and as passivation
and insulation layers in interconnect structures to encapsulate the
interconnecting lines from each other. In the latter example, a very low
dielectric constant is the optimum for the overall device performance.
There are many materials which provide better electrical behavior than
![]() , but none of them can be as reliably produced within existing
economical limits as
, but none of them can be as reliably produced within existing
economical limits as
![]() .
Therefore, the
.
Therefore, the
![]() technology is very commonly used and has generated a
considerably big market for such fabrication machinery, which even further
reduces its COO.
If new material compounds have to be considered in terms of fabrication,
additional materials have to be acquired, which are mostly very rare in high
purity.
Furthermore, the deposition and etching of such materials often requires new
chemical environments and new machinery to handle these chemical reactions.
technology is very commonly used and has generated a
considerably big market for such fabrication machinery, which even further
reduces its COO.
If new material compounds have to be considered in terms of fabrication,
additional materials have to be acquired, which are mostly very rare in high
purity.
Furthermore, the deposition and etching of such materials often requires new
chemical environments and new machinery to handle these chemical reactions.
Despite of the huge costs, the enhanced electrical requirements given by the
semiconductor road map demand the introduction of new materials which have
either lower or higher relative dielectric constants
![]() to fulfill the
industry's needs for future down scaling.
to fulfill the
industry's needs for future down scaling.
Sofar, enormous efforts have been made to supply the newly developed technology
nodes with novel materials that require only minor changes to the standard
![]() process flow.
Material types, which have succeeded in reducing COO are the
low-
process flow.
Material types, which have succeeded in reducing COO are the
low-![]() and
high-
and
high-![]() materials. The offer different
materials. The offer different
![]() values compared to
values compared to
![]() and are used to adjust the capacitive coupling through material selection.
and are used to adjust the capacitive coupling through material selection.
The dielectrics can be grouped according to their chemical structure in oxides, nitrides, carbides, halogenides, polymers, and organic materials. In addition, there are plenty of mixtures and doped material which provide advantageous material properties for certain purposes.
The group of oxides include the well known compounds
![]() ,
,
![]() , and
germanium oxide which can be either
, and
germanium oxide which can be either
![]() or
or
![]() where
germanium dioxide is thermally more stable.
Other commonly used oxides for new semiconductor structures are
where
germanium dioxide is thermally more stable.
Other commonly used oxides for new semiconductor structures are
![]() ,
,
![]() ,
,
![]() , and
, and
![]() which are mainly used as
high-
which are mainly used as
high-![]() materials within FEOL
structures like gate stacks for transistors or capacitors for memory cells.
Special types of oxides are the
high-
materials within FEOL
structures like gate stacks for transistors or capacitors for memory cells.
Special types of oxides are the
high-![]() compounds Perovskites and lead
zirconium titanites (PZT). They provide high values of
compounds Perovskites and lead
zirconium titanites (PZT). They provide high values of
![]() but have a very
limited thermal budget because above the
CURIE2.37 temperature the spontaneous polarization
vanishes according to a mechanical relaxation of the crystals.
but have a very
limited thermal budget because above the
CURIE2.37 temperature the spontaneous polarization
vanishes according to a mechanical relaxation of the crystals.
The nitride group includes
![]() ,
,
![]() , and
, and
![]() which excels with their
hardness. Unfortunately, the member materials are quite brittle compared to
most of the oxides. Important advantages of nitrides are that nitrides can be built on
top of a metal layer and that according to the stability of the nitride
compound, the nitride layer can be used to seal certain regions for instance to
avoid the diffusion of a particular metal to its surrounding semiconducting or
insulating materials.
which excels with their
hardness. Unfortunately, the member materials are quite brittle compared to
most of the oxides. Important advantages of nitrides are that nitrides can be built on
top of a metal layer and that according to the stability of the nitride
compound, the nitride layer can be used to seal certain regions for instance to
avoid the diffusion of a particular metal to its surrounding semiconducting or
insulating materials.
Carbides are another group of dielectrics where
![]() is the most important
representative. Because its advantageous crystal structure, this material can be
used as a substrate material like Si, Ge, or
is the most important
representative. Because its advantageous crystal structure, this material can be
used as a substrate material like Si, Ge, or
![]() . However,
. However,
![]() is very
brittle, extremely hard, and chemically very robust. Hence, it is also used for
BEOL structures for instance as etch stop layers in interconnect stacks.
is very
brittle, extremely hard, and chemically very robust. Hence, it is also used for
BEOL structures for instance as etch stop layers in interconnect stacks.
Beside the already mentioned materials types, there are plenty of polymers and organic
compounds which include polyimide, poly-tetra-fluorine-ethylene (PTFE),
organosicate glasses, and other polymers. Those materials are often used as
low-![]() materials in BEOL structures as interlayer dielectrics (ILD) and
some even as substitute for semiconducting materials.
materials in BEOL structures as interlayer dielectrics (ILD) and
some even as substitute for semiconducting materials.
For BEOL structures dielectric layers are often doped to improve particular
properties such as to harden the material compound, decrease the relative
permittivity, or to reduce the diffusion constant for a certain atom species [148].
Typical representatives for this type are
![]() ,
,
![]() ,
,
![]() ,
,
![]() . They appear in the interconnect structures of leading edge high
performance devices.
. They appear in the interconnect structures of leading edge high
performance devices.
A critical issue in alternative materials is their temperature stability
both during fabrication and during operation.
For instance the phase stage of the Perovskites and PZT crystal structures
that provides the high
![]() value is only thermally stable below the CURIE
temperature
value is only thermally stable below the CURIE
temperature
![]() . For these materials the CURIE temperature determines the
temperature limit for operation and the thermal budget during device
fabrication.
Figure 2.11 shows the principal assembly of a unit cell of a certain
PZT material. In the mechanically relaxed stage, the crystal shows a
face centered cubic structure where the Ti atom is exactly located in the center
of the cubic unit cell.
. For these materials the CURIE temperature determines the
temperature limit for operation and the thermal budget during device
fabrication.
Figure 2.11 shows the principal assembly of a unit cell of a certain
PZT material. In the mechanically relaxed stage, the crystal shows a
face centered cubic structure where the Ti atom is exactly located in the center
of the cubic unit cell.
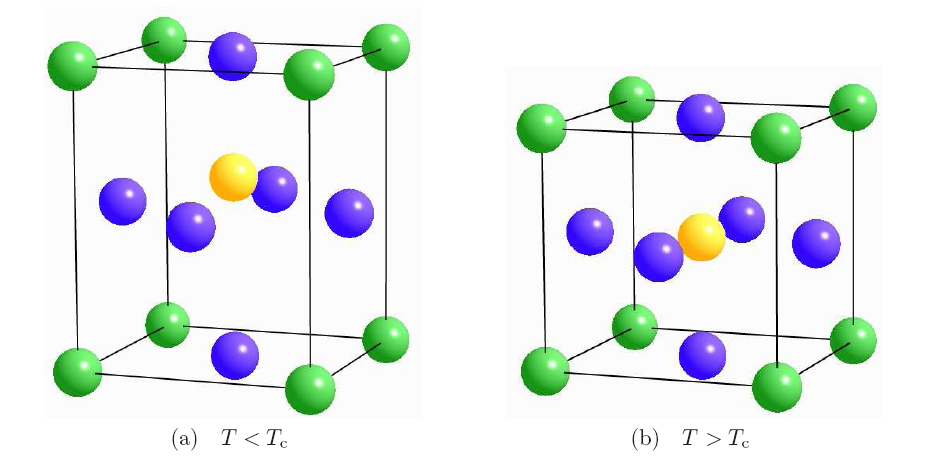 |
This is demonstrated in Figure 2.11 where an applied electric field in
the vertical direction enables the Ti atom to slip from the upper side to the
lower side of the center of the unit cell. This effect of flipping the Ti atom
provides the high
![]() value.
However, with every flip of the Ti atom, energy is absorbed by the crystal
and causes hysteresis loss and with increasing number of flips the
value.
However, with every flip of the Ti atom, energy is absorbed by the crystal
and causes hysteresis loss and with increasing number of flips the
![]() number will be slightly reduced due to mechanical relaxations.
Nevertheless, the number of possible flips is enormous according to the current
reliability concerns according to the ITRS.
But if the temperature is increased above a certain threshold value (CURIE
temperature), the thermal energy is sufficient for the advantageous crystal
structure to mechanically relax. As a consequence, the high
number will be slightly reduced due to mechanical relaxations.
Nevertheless, the number of possible flips is enormous according to the current
reliability concerns according to the ITRS.
But if the temperature is increased above a certain threshold value (CURIE
temperature), the thermal energy is sufficient for the advantageous crystal
structure to mechanically relax. As a consequence, the high
![]() vanishes and
drops back to approximately 1 in the global energetic minimum of this crystal
structure.
vanishes and
drops back to approximately 1 in the global energetic minimum of this crystal
structure.
Low-![]() materials can be used to reduce capacitive coupling like
cross talk or influence charges in adjacent interconnect lines.
Materials with
materials can be used to reduce capacitive coupling like
cross talk or influence charges in adjacent interconnect lines.
Materials with
![]() values lower than 2.5 are called extreme
low-
values lower than 2.5 are called extreme
low-![]() (ELK)
materials.
Typical ELK materials reach values around 2.4 by using doped
(ELK)
materials.
Typical ELK materials reach values around 2.4 by using doped
![]() .
Examples are
.
Examples are
![]() [149,150,148,151],
[149,150,148,151],
![]() , or
, or
![]() [152,153]. Alternatively, values in the
regime between 1.6 and 1.9 have been reported using air
gaps [154,155,156].
Polymers like aromatic polymers [21] reach values of
[152,153]. Alternatively, values in the
regime between 1.6 and 1.9 have been reported using air
gaps [154,155,156].
Polymers like aromatic polymers [21] reach values of
![]() . A typical range for organic silicate glasses OSG is
. A typical range for organic silicate glasses OSG is
![]() [21], whereby the low values for the latter materials can
be obtained if a porous low methyl variant of OSG is used [21].
[21], whereby the low values for the latter materials can
be obtained if a porous low methyl variant of OSG is used [21].
As additional layers for etch stop and passivation purposes, the materials
![]() and
and
![]() can be used where carbon doped nitride offers a lower
can be used where carbon doped nitride offers a lower
![]() than the commonly used
than the commonly used
![]() [151].
To account for the high mechanical stress in these material stacks used in BEOL
structures, additional layers of
[151].
To account for the high mechanical stress in these material stacks used in BEOL
structures, additional layers of
![]() can significantly reduce the mechanical
stress but have higher
can significantly reduce the mechanical
stress but have higher
![]() values than
values than
![]() [157,158].
[157,158].