3.5 Volume Expansion

The models which consider the thermal volume expansion have similar problems with the material structure as the models for the electrical and electrical conductivities. However, the thermal volume expansion coefficient is estimated with an equation given for bulk material as

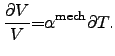$$\frac{\partial V}{V} {=}{\alpha^{\mathrm{mech}}}\; \partial T.$$ (3.22)

A rigorous mechanical investigation would require the appropriate volume expansion coefficients for the contributing materials. Those parameters can be either obtained from rigorous Monte Carlo calculations or from measurements. The coefficients given in Tab. 3.4 were obtained from measurements of bulk materials and give sufficient approximations. The microelectronic devices considered in this thesis show a slightly different behavior because the volume expansion described in (3.22) is mechanically constricted by additional material layers. The mechanical equation system is applied to materials which are embedded in rather stiff bulk material which normally do not allow expansion. This results in mechanically highly stressed material regions, especially if high temperature gradients are present. The thinner the material layers are the more sensitive they are and tend to relax by cracking. A crack in a layer often results in a fatal failure of the complete system, which is assumed to be the worst case. To avoid this type of failure, an appropriate investigation is required which also includes the mechanical subsystem.

Table 3.4: Typical values for thermal expansion coefficients of various materials.

Material	${\alpha^{\mathrm{mech}}}$ [1/K]	References
Al	$2.5{\times}10^{-5}$	[200]
Cu	$1.4-4.92{\times}10^{-5}$	[142,79]
Mo	$1.5{\times}10^{-5}$	[142]
W	$0.45-1.3{\times}10^{-5}$	[142,79]
Ta	$0.65-1.92{\times}10^{-5}$	[200,142]
Ti	$7.6-9.8{\times}10^{-6}$	[79]
Ag	$5.7{\times}10^{-5}$	[142]
Au	$4.32{\times}10^{-5}$	[142]
Al	$6.78{\times}10^{-5}$	[142]
Si	$2.33{\times}10^{-6}$	[79]
${\mathrm{polySi}}$	$2.6{\times}10^{-6}$	[201]
$\mathrm{SiO_2}$	$0.25-1.4{\times}10^{-6}$	[201,25,79]
${\mathrm{Si_3N_4}}$	$1.1-4.2{\times}10^{-6}$	[25,79]
${\mathrm{Al_2O_3}}$	$5.6-7.1{\times}10^{-6}$	[25,79]
${\mathrm{TiN}}$	$6.5{\times}10^{-6}$	[200]

If a block consisting of different materials tends to expand it is limited in its movement by the surrounding materials in which it is embedded. Hence, mechanical stress develops according to the values given in Tab. 3.4 for the thermal volume expansion coefficients.

The relation (2.110) considers expansion as well as contraction and torsion, thus, all phenomena where atoms are moved. However, if movements of atoms or atom clusters have to be considered, the mesh for those regions is very critical and can cause tremendous problems. For instance, in a region where a layer is contracted due to surrounded materials with a higher stiffness, the mesh is contracted as well. Due to limited numerical precision or approximations made in the material models, a single mesh point might move through a mesh edge between two other mesh points. This results in negative volumes and negative coupling coefficients in the finite element method and causes numerical problems, because the resulting system matrices are no longer positive definite and the solver have commonly severe convergence problems or even fails.