The NEWTON iteration scheme offers a simple but very powerful root-search
algorithm with a quadratic convergence property, if the initial guess is located
within a confidence interval (domain) near the root.
Hence the NEWTON iteration scheme provides a local root search for a function
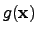 and a local optimization strategy for
and a local optimization strategy for
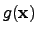 if this function
represents a spatial derivative of an objective function
if this function
represents a spatial derivative of an objective function
![$\displaystyle {\mathbf{{x}}}_{n+1} - {\mathbf{{x}}}_n {=}\big[\nabla g({\mathbf{{x}}}_n)\big]^{-1}\cdot g({\mathbf{{x}}}_n), n \ge 0.$](img753.png) |
(4.17) |
The NEWTON iteration method can be applied for the optimization
problem (4.1), where the minimum/maximum search of the score function
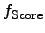 is equivalent to the root search of the spatial derivative of the
score function if the function
is equivalent to the root search of the spatial derivative of the
score function if the function
 substituted
to (4.17). Hence, the optimization as a root search reads
substituted
to (4.17). Hence, the optimization as a root search reads
![$\displaystyle {\mathbf{{x}}}_{n+1} - {\mathbf{{x}}}_n {=}\big[\nabla \left(\nab...
...)\right)\big]^{-1}\cdot \nabla {f_{\mathrm{Score}}}({\mathbf{{x}}}_n), n \ge 0.$](img755.png) |
(4.18) |
In (4.17) and (4.18)
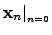 represents the used-defined
initial value,
represents the used-defined
initial value,
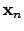 is the current value of the NEWTON iteration, and
is the current value of the NEWTON iteration, and
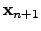 is the next value which is improved by the local derivative for
the objective function.
An additional disadvantage of this method is the requirement of the second
derivative of the objective function. If higher dimensional parameter spaces
have to be considered, the computational effort can be enormous compared to the
nominal number of parameter evaluations.
To improve the convergence property the NEWTON optimization algorithm line
searches are used.
If the curvature of the function is positive, the optimum found is a local
minimum, and otherwise a maximum.
is the next value which is improved by the local derivative for
the objective function.
An additional disadvantage of this method is the requirement of the second
derivative of the objective function. If higher dimensional parameter spaces
have to be considered, the computational effort can be enormous compared to the
nominal number of parameter evaluations.
To improve the convergence property the NEWTON optimization algorithm line
searches are used.
If the curvature of the function is positive, the optimum found is a local
minimum, and otherwise a maximum.
Stefan Holzer
2007-11-19
![]() and a local optimization strategy for
and a local optimization strategy for
![]() if this function
represents a spatial derivative of an objective function
if this function
represents a spatial derivative of an objective function