4. Optimization for Technology CAD
``Man darf nicht das, was uns unwahrscheinlich und
unnatürlich
erscheint, mit dem verwechseln, was absolut unmöglich
ist.''
Carl Friedrich Gauß4.1
THIS chapter first discusses the different optimization
techniques and strategies that are commonly used in modern optimization
applications. The second part of this chapter deals with the industrial
requirements for optimization as well as its challenges for TCAD
applications. The third part shows the need of an optimization framework and the
resulting concepts which fulfills the presented requirements.
In this work the term optimization is used as a search for a minimal or maximal
value for an objective function (also called score function) within
certain defined constraints.
It is a widely used practice that optimization problems are formulated as
a minimization task of an objective score function
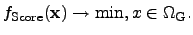 |
(4.1) |
To perform a maximum search, the formalism can be transformed
to a minimum search for negative values of an objective score function [219]
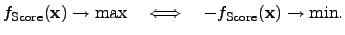 |
(4.2) |
Despite of the different score functions for the
optimization, the mathematical convergence criteria for both
optimization algorithms remain valid [219]4.2.
The optimization problems discussed in this thesis are finite-dimensional
optimizations of the following type: A given 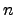 -dimensional variable vector
-dimensional variable vector
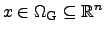 of an
of an 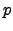 -dimensional objective score
function
-dimensional objective score
function
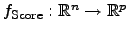 has to be optimized
globally in order to obtain a resulting vector
has to be optimized
globally in order to obtain a resulting vector
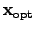 which minimizes the value
of the score function in a certain domain
which minimizes the value
of the score function in a certain domain
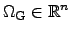 .
Equation (4.1) can also be expressed by using the following equivalent notation:
.
Equation (4.1) can also be expressed by using the following equivalent notation:
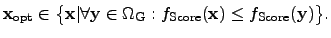 |
(4.3) |
In this definition, the function
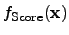 denotes a continuous objective score function
which has to be minimized. To determine a mathematically suitable criterion for
minimization, the objective function
denotes a continuous objective score function
which has to be minimized. To determine a mathematically suitable criterion for
minimization, the objective function
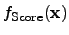 has to apply a metric which
maps the simulation result in a scalar-valued quantity.
has to apply a metric which
maps the simulation result in a scalar-valued quantity.
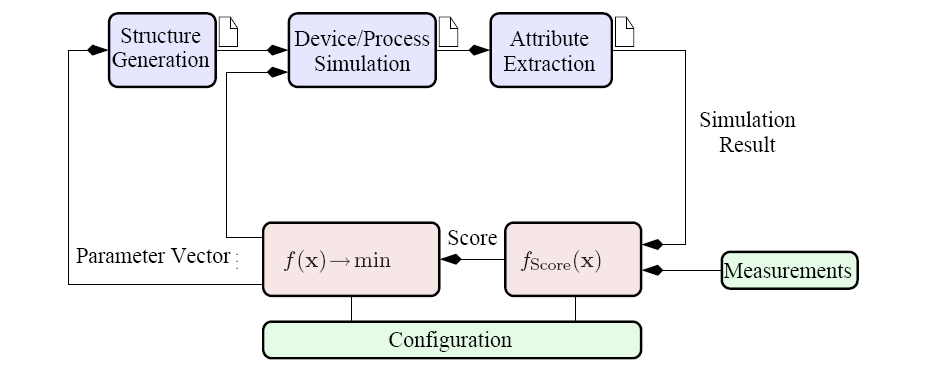
Figure 4.1:
Generic optimization loop for multiple purposes.
 |
The industrial requirements requires an objective score function
of the form
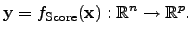 |
(4.4) |
However, this type of optimization would require optimization tools that are
capable to operate with PARETO4.3 sets which is not commonly
available in optimization tools.
To overcome this kind of problem, a weighted norm can be applied to the score
function and reads
![$\displaystyle {f_{\mathrm{Score}}({\mathbf{{x}}})}{=}\sqrt[p]{\sum_{i=0}^{p} \a...
...{\mathrm{Sim},i}({\mathbf{{x}}})\vert^p} : \mathbb{R}^n \rightarrow \mathbb{R},$](img719.png) |
(4.5) |
where the result of this score functions is a real number, which can be
optimized using the property that
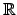 is an ordered field.
If the weight parameters
is an ordered field.
If the weight parameters 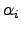 are set to 1, (4.5) can be written as
are set to 1, (4.5) can be written as
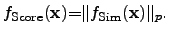 |
(4.6) |
In typical TCAD applications such objective score functions represent
sequences of simulation software tools and therefore
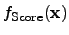 can also
include some necessary post-processing steps.
A typical data flow of an optimization run is shown in Figure 4.1 where
certain different input parameters can be applied to each simulation tool
separately. In this depicted example, the simulation flow consists of a tool for
the generation of the device geometry, the device simulator, and at the end a tool
for the extraction of objective parameters from a finite-dimensional simulation
result in order to compare it with reference data, which can be either constant
values, analytical functions, or quantities in tables obtained from
measurements.
can also
include some necessary post-processing steps.
A typical data flow of an optimization run is shown in Figure 4.1 where
certain different input parameters can be applied to each simulation tool
separately. In this depicted example, the simulation flow consists of a tool for
the generation of the device geometry, the device simulator, and at the end a tool
for the extraction of objective parameters from a finite-dimensional simulation
result in order to compare it with reference data, which can be either constant
values, analytical functions, or quantities in tables obtained from
measurements.
In order to limit the optimum search to a certain domain and to weight or
exclude certain parameter constellations, the input parameter space can be
constrained by lower and upper bounds as well as by a finite number of
constraint functions.
In the following chapter
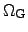 denotes a convex4.4 and closed
finite-dimensional domain
denotes a convex4.4 and closed
finite-dimensional domain
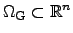 which can be
further constrained by functions
which can be
further constrained by functions 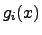 which yields in the most general case
a non-convex shape and can be expressed as
which yields in the most general case
a non-convex shape and can be expressed as
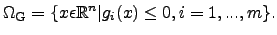 |
(4.7) |
The constraint functions 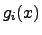 can map for instance some physical constraints
to the input parameter domain, represent some technological or economical
constraint from the fabrication processes, or these functions can be used to
avoid parameter constellations which are not allowed, either by specifications
or due to patent laws.
However, these functions have to be individually chosen for a particular
optimization problem.
Constraints for
can map for instance some physical constraints
to the input parameter domain, represent some technological or economical
constraint from the fabrication processes, or these functions can be used to
avoid parameter constellations which are not allowed, either by specifications
or due to patent laws.
However, these functions have to be individually chosen for a particular
optimization problem.
Constraints for
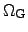 can be applied a-priori in contrast to constraints
for output parameters. Therefore, the resulting domain for valid output
parameters
can be applied a-priori in contrast to constraints
for output parameters. Therefore, the resulting domain for valid output
parameters
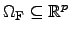 is defined as the physical
feasible values and the corresponding constraint function reads
is defined as the physical
feasible values and the corresponding constraint function reads
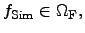 |
(4.8) |
where the valid values of the output domain
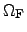 are given by the nested
function of the score function
are given by the nested
function of the score function
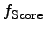 applied to the final results of the
function
applied to the final results of the
function
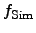 which describes the sequence of the different
simulation tools used.
which describes the sequence of the different
simulation tools used.
While a-priori constraints limit the search domain only, a-posteriori
constraints restrict the simulation results, which requires to calculate a
complete simulation sequence to obtain a single result. This is thus very costly
in time.
Therefore, one tries to transform the constraints for
the output in constraints for input parameters.
For some cases, where the constraints of simulation results have to be included
into the constraint functions, an estimation can be performed to approximate the
simulation results in advance.
If the calculations of the original function is very time-consuming compared to
the time for evaluating the approximation, this method provides the benefit of
saving time by excluding certain a-priori known not valid simulation
results.
With the domains (4.7) and (4.8) the initially
constrained minimization problem (4.1) can be reformulated by using
barrier or penalty functions
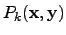 in order to obtain an unconstrained
surrogate optimization problem [219,220].
in order to obtain an unconstrained
surrogate optimization problem [219,220].
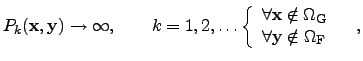 |
(4.9) |
which provide the possibility to use the original optimization framework with
minor changes which can be specified by the user.
In (4.9)
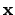 symbolizes the input parameters and
symbolizes the input parameters and
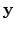 the output
parameters or the results of the simulation and the score function. The barrier
and penalty functions try to account for the behavior of the output
the output
parameters or the results of the simulation and the score function. The barrier
and penalty functions try to account for the behavior of the output
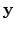 as
accurately as possible in order to save computation time. Then the penalty
problem reads
as
accurately as possible in order to save computation time. Then the penalty
problem reads
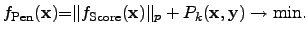 |
(4.10) |
To conveniently apply such functions to a particular problem, the penalty
function can be adapted to user defined constraints. For instance, there exist
several different approaches for barrier and penalty terms. In the following, the
barrier and penalty functions 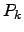 are defined using a sequence of
penalty parameters
are defined using a sequence of
penalty parameters 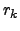 , where
, where
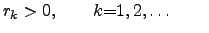 and and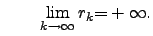 |
(4.11) |
Since the transition of
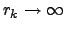 in (4.11) is numerically
impossible, various finite approximations have been proposed in literature.
However, the use of large numbers can result in serious convergence problems,
because of the numerical calculations of the gradients when regions are
considered which are located very close to the domain boundaries.
in (4.11) is numerically
impossible, various finite approximations have been proposed in literature.
However, the use of large numbers can result in serious convergence problems,
because of the numerical calculations of the gradients when regions are
considered which are located very close to the domain boundaries.
The formulation for barrier and penalty functions often considers a certain
margin of the valid parameter domain. To prevent the search algorithm from moving
too close to the domain boundary, a barrier function is applied that reaches the
value infinity at the boundary. The penalty function charges a certain fine for
the function if the search algorithm is outside of the specified domain.
The inexact penalty functions have are vanishing inside the allowed domain.
There are several methods to implement such barrier and penalty functions:
- The exact penalty function [221,222,223] vanishes inside the
specified parameter domain and reaches a certain value greater zero outside
the domain:
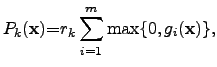 |
(4.12) |
where the corresponding constraint functions 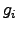 apply with
apply with
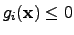 inside the
valid parameter domain and
inside the
valid parameter domain and 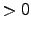 outside.
outside.
- The exact quadratic penalty function [224,225] is quite similar to
the previous one, but shows generally a quadratic increase with the distance
from the domain boundary:
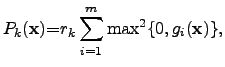 |
(4.13) |
where the corresponding constraint functions 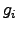 apply. Again,
apply. Again,
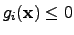 inside the
valid parameter domain and
inside the
valid parameter domain and 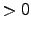 outside.
outside.
- A logarithmic barrier function [226,227,228] offers the
possibility of directing the parameter search to particular subdomains, in
which the score function is superposed by a logarithmic function in the whole
domain. Hence, the minimum of the sum of the score function and the
logarithmic barrier function is located in the subdomain in which the optimum
is. At the boundaries and outside the domain, the barrier function reaches
infinity according to the definition of
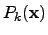 :
:
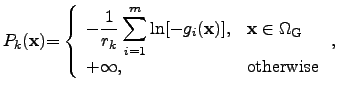 |
(4.14) |
where the corresponding constraint functions 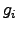 apply for
apply for
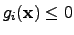 inside the
valid parameter domain and
inside the
valid parameter domain and 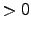 outside.
outside.
- With an inverse barrier function [224], the search region inside the
parameter domain can be predefined similarly to the logarithmic barrier
function, but with a differently shaped approximation:
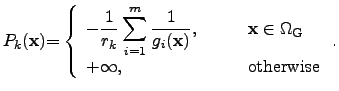 |
(4.15) |
Here, the constraint functions 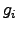 are applied, where
are applied, where
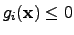 inside the
valid parameter domain and
inside the
valid parameter domain and 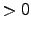 outside.
outside.
- An inexact exponential penalty function [229] offers an efficient method to
priorize a particular subdomain of the parameter domain without dealing with
infinity. However, the value of the barrier function increases rapidly when the
search algorithm leaves the valid parameter domain.
![$\displaystyle P_k({\mathbf{{x}}}) {=}r_k \displaystyle\sum^{m}_{i=1}\exp[r_k g_i({\mathbf{{x}}})],$](img749.png) |
(4.16) |
where the constraint functions satisfy
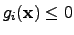 inside the valid parameter domain and
inside the valid parameter domain and 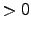 outside.
outside.
However, the user has always to choose the appropriate barrier or penalty
functions in order to account for his particular needs and to check the convergence
behavior of the whole optimization algorithm in advance.
For instance if the score function and the contributions from the barrier and
penalty function differ by many orders of magnitude, the discretization and
gradient calculations algorithm of the optimizer might run into numerical
problems in terms of precision and accuracy.
According to the principal behavior of the score function within the optimization
problem, an appropriate barrier or penalty function modifies the original
optimization problem in the same way as the score function would, but
provides an additional term to the score function which allows to exclude
certain domains from the original parameter space or to priorize certain
subdomains for example if several optimal values are expected.
Since many of the available optimization strategies do not inherently support
constraint functions, additional barrier and penalty function are often used in
non-linear optimization problems where only a certain set of optimization
strategies are available for utilization with in a framework.
Subsections
Stefan Holzer
2007-11-19
![]() denotes a convex4.4 and closed
finite-dimensional domain
denotes a convex4.4 and closed
finite-dimensional domain
![]() which can be
further constrained by functions
which can be
further constrained by functions ![]() which yields in the most general case
a non-convex shape and can be expressed as
which yields in the most general case
a non-convex shape and can be expressed as
![]() in order to obtain an unconstrained
surrogate optimization problem [219,220].
in order to obtain an unconstrained
surrogate optimization problem [219,220].
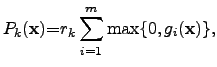
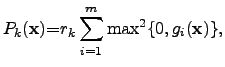
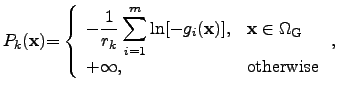
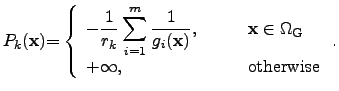
![$\displaystyle P_k({\mathbf{{x}}}) {=}r_k \displaystyle\sum^{m}_{i=1}\exp[r_k g_i({\mathbf{{x}}})],$](img749.png)