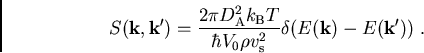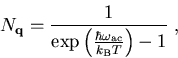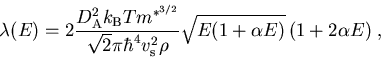

Next: 1.4.1.2 Optische Zwischentalstreuung
Up: 1.4.1 Phononenstreuung
Previous: 1.4.1 Phononenstreuung
Da bei akustischen Gitterschwingungen die Auslenkung benachbarter
Atome in gleicher Richtung erfolgt, ist für die Deformation der Gradient der Elongation 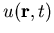 ausschlaggebend. Man wählt daher den Ansatz [JL89]
ausschlaggebend. Man wählt daher den Ansatz [JL89]
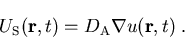 |
(1.70) |
Nach Auswertung der Übergangswahrscheinlichkeit mit der goldenen Regel von
Fermi lautet die Streurate aufgrund quantisierter akustischer
Gitterschwingungen
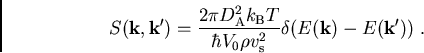 |
(1.71) |
Die Schallgeschwindigkeit im Halbleiter wird mit 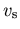 bezeichnet und die Dichte
des Materials mit
bezeichnet und die Dichte
des Materials mit 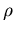 . Ferner wird die temperaturabhängige Besetzung der
Phononen im thermodynamischen
Gleichgewicht, gegeben durch die Bose-Einstein Statistik,
. Ferner wird die temperaturabhängige Besetzung der
Phononen im thermodynamischen
Gleichgewicht, gegeben durch die Bose-Einstein Statistik,
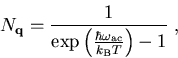 |
(1.72) |
für einen kleinen Impuls 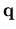 derart angenähert, daß für die
Besetzungszahl mit der Phononenenergie
derart angenähert, daß für die
Besetzungszahl mit der Phononenenergie 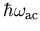 gilt:
gilt:
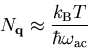 |
(1.73) |
Die Dispersionsrelation wird als
linear angenommen und weiters wird, da die Phononenenergie gering ist,
dieser Streumechanismus als elastisch angenommen. Man erhält für die
totale Streurate für ein nicht-parabolisches Band
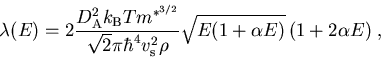 |
(1.74) |
wobei zwischen Emission und Absorption nicht mehr unterschieden wird.
Sowohl der polare als auch der azimutale Winkel sind isotrop verteilt.
Symmetriebeziehungen, die im besonderen die Kristallstruktur behandeln, zeigen,
daß in Silizium diese Streuung nur in longitudinalen Moden auftritt. Aufgrund
des kleinen, vernachlässigbaren Energieübertrags und der
Symmetrieauswahlregeln verbleiben Elektronen bei diesem Streuprozeß im selben
Band. Akustische Phononen haben also Innertal-Charakter
[JL89].


Next: 1.4.1.2 Optische Zwischentalstreuung
Up: 1.4.1 Phononenstreuung
Previous: 1.4.1 Phononenstreuung
Kaiblinger-Grujin Goran
1997-12-06