|
The empirical tight-binding model is a standard, convenient, and accurate method for
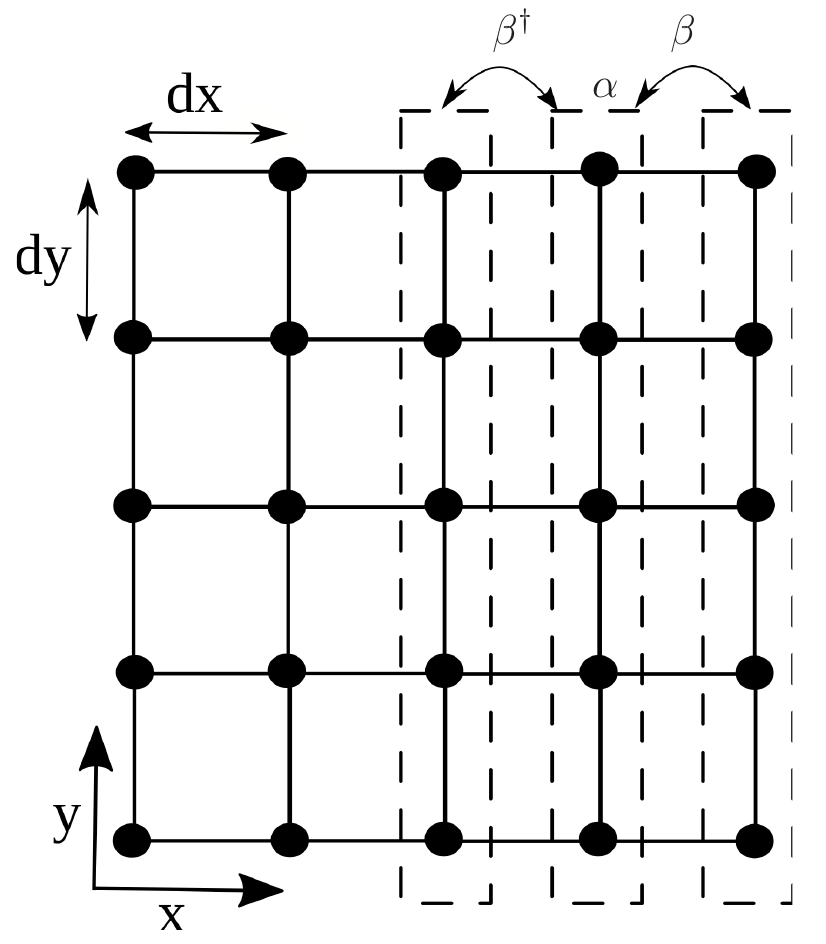
calculating the electronic structure of semiconductors. It is also referred to as Bloch or linear combination of atomic orbitals (LCAO) method [31]. The Hamiltonian matrix for a simplified 2D system, using the TB method is described as follows: The 2D structure in Fig. 2.1 is composed of ![]() chains of lattice points (i.e. atomic sites), each chain with
chains of lattice points (i.e. atomic sites), each chain with ![]() sides. Assuming that each point is represented by one basis orbital, the Hamiltonian matrix will have the size
sides. Assuming that each point is represented by one basis orbital, the Hamiltonian matrix will have the size
![]() , and is given by:
, and is given by:
|
The only change, here, is in the submatrices
![]() and
and
![]() , which now include the self energies of the left and right contacts. In the case of periodic boundary conditions, the bandstructure is calculated by considering the unit cell (index
, which now include the self energies of the left and right contacts. In the case of periodic boundary conditions, the bandstructure is calculated by considering the unit cell (index ![]() ) of the lattice, connected to the neighboring unit cells (index
) of the lattice, connected to the neighboring unit cells (index ![]() ) using the matrix elements
) using the matrix elements ![]() . For example, as indicated in the structure of Fig. 2.1, once periodic boundary conditions are applied along the
. For example, as indicated in the structure of Fig. 2.1, once periodic boundary conditions are applied along the ![]() -axis, then
-axis, then
![]() and
and
![]() for all
for all
![]() . The bandstructure of the lattice is then obtained by calculating the eigenvalues of the Hamiltonian as:
. The bandstructure of the lattice is then obtained by calculating the eigenvalues of the Hamiltonian as:
![$\displaystyle [h(k)]=\sum_{m}H_{nm}\mathrm{e}^{i\vec{k}\cdot(\vec{d}_m-\vec{d}_n)}$](img134.png) |
(2.6) |
|
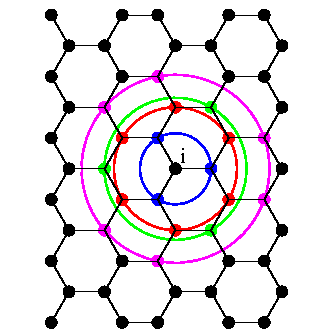
In the case of graphene, a third nearest neighbor tight-binding model is used to describe
its electronic structure. In this case, the particular atom ![]() and its nearest neighbor atoms are shown in Fig. 2.2. The hopping parameter between two nearest atoms separated by distance
and its nearest neighbor atoms are shown in Fig. 2.2. The hopping parameter between two nearest atoms separated by distance ![]() is
is
![]() . The tight-binding parameter of the third-nearest neighbor atoms located
. The tight-binding parameter of the third-nearest neighbor atoms located ![]() away from each other is
away from each other is
![]() [34]. The hopping parameter for the second nearest-neighbor is assumed to be
[34]. The hopping parameter for the second nearest-neighbor is assumed to be
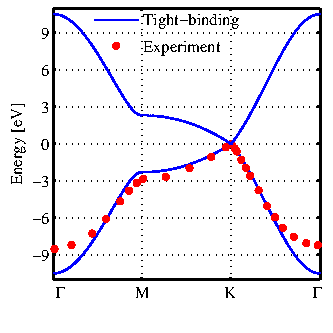
![]() . The bandstructure of graphene along the high-symmetry band line is shown in Fig. 2.3. The tight-binding results are in good agreement with experimental data taken from [33], in particular
around the Fermi energy
. The bandstructure of graphene along the high-symmetry band line is shown in Fig. 2.3. The tight-binding results are in good agreement with experimental data taken from [33], in particular
around the Fermi energy
![]() which dominates the electrical properties. As shown in Ref. [34] this method can capture the details of the bandstructure of graphene-based nanostructures. The tight-binding model with calibrated parameters provides band-gap and subband-edge energies in excellent agreement with first-principles calculations [34].
which dominates the electrical properties. As shown in Ref. [34] this method can capture the details of the bandstructure of graphene-based nanostructures. The tight-binding model with calibrated parameters provides band-gap and subband-edge energies in excellent agreement with first-principles calculations [34].