| N | |
|
|
|---|---|---|---|
| 1 | 365.0 | 245.0 | 98.2 |
| 2 | 88.0 | -32.3 | -4.0 |
| 3 | 30.0 | -52.5 | 1.5 |
| 4 | -19.2 | 22.9 | -5.8 |
| N | |
|
|
|---|---|---|---|
| 1 | 365.0 | 245.0 | 98.2 |
| 2 | 88.0 | -32.3 | -4.0 |
| 3 | 30.0 | -52.5 | 1.5 |
| 4 | -19.2 | 22.9 | -5.8 |
The FCM model we employ involves a fourth nearest-neighbor approximation (see
Fig. 2.2). The force constant tensor describing the coupling between the ![]() and the
and the ![]() carbon atom, which are the
carbon atom, which are the ![]() nearest-neighbor of each other, is given by:
nearest-neighbor of each other, is given by:
The motion of the atoms can be described by a dynamic matrix as:
Here, we assume that the graphene sheet is located in the ![]() plane and that
plane and that
![]() represents the angle between the
represents the angle between the ![]() -axes and the bond between the
-axes and the bond between the ![]() and
and ![]() carbon atom. The phononic bandstructure can be calculated by solving the eigen-value problem described by:
carbon atom. The phononic bandstructure can be calculated by solving the eigen-value problem described by:
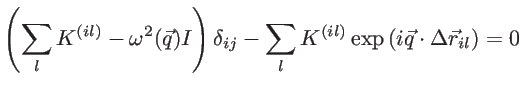 |
(2.11) |
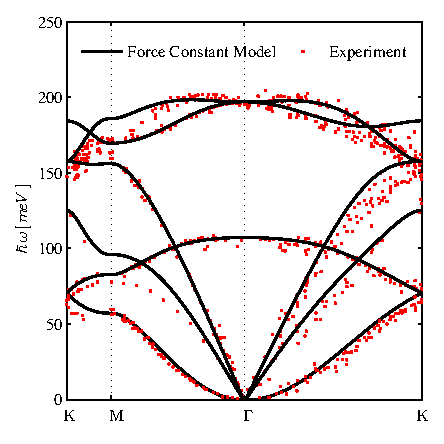
The phononic bandstructure of graphene shown in Fig. 2.4 is evaluated using the fourth nearest-neighbor FCM with force constants given in Table. 2.1. This method relies on twelve fitting parameters that determine the force constants, which are extracted from experiments. To validate the model, we present the experimental phonon bandstructure results from Refs. [40,43]. As expected, the result is in good agreement with the experimental data (see Fig. 2.4), especially for the low phonon frequencies, which are the most important ones in determining the thermal conductivity.
|
Because the model relies on empirical parameters fitted to experiments, it is much more computationally efficient compared to other atomistic formalisms, such as the valence force field (VFF) method. In the VFF method, for example, the force constants for each atom in the unit cell are calculated, and the simulation time is dominated by the dynamic matrix construction [39]. The approximation in that method comes from the parameters used in the evaluation of the potential energy. For FCM, since force constants are empirical parameters, the construction time of the dynamic matrix is negligible, which makes the computation much more efficient. The simulation time is determined by the solution of the eigenvalue problem. In the graphene lattice this results in 18 neighbors for each atom as shown in Fig. 2.2. In FCM we assume that there is a spring between each carbon atom and its 18 neighbors. This number is reduced in the case of boundary atoms with less nearest-neighbors.