


Next: 2.4.2 Boltzmann Transport Equation
Up: 2.4 Phonon Transport
Previous: 2.4 Phonon Transport
Contents
In semiconductors, the largest component of the heat current is due to the phonon transport. Using the Landauer theory for phonon transport, the heat flow is proportional to the phonon transmission function
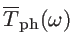 , the Bose-Einstein distribution function
, the Bose-Einstein distribution function 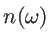 of source and drain contacts, and the phonon energy/frequency
of source and drain contacts, and the phonon energy/frequency 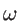 as:
as:
![$\displaystyle I_q=\frac{1}{h}\int_{0}^{+\infty} \overline{T}_{\mathrm{ph}}(\ome...
...left [ n_{\mathrm{s}}(\omega)-n_{\mathrm{d}}(\omega) \right ] \ d(\hbar \omega)$](img292.png) |
(2.52) |
In the linear response regime of the Landauer theory the heat current is proportional to the temperature difference by:
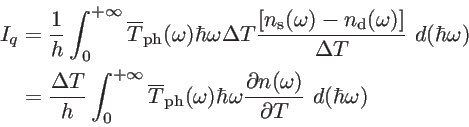 |
(2.53) |
This can alternatively be written as:
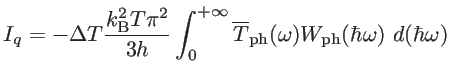 |
(2.54) |
where the phononic window function is given by [57]:
![\begin{displaymath}\begin{split}W_{\mathrm{ph}}(\hbar \omega)&=-\frac{3}{\pi^2}\...
...ar \omega}{2 k_{\mathrm{B}}T}\right ) \right ]^{-2} \end{split}\end{displaymath}](img295.png) |
(2.55) |
As
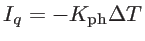 , one can express the lattice contribution to the thermal conductance as [58]:
, one can express the lattice contribution to the thermal conductance as [58]:
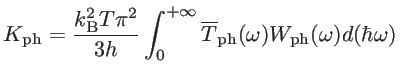 |
(2.56) |
To extract the ballistic phonon transmission
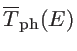 in Eq. 2.56, similar to the electronic quantities (Eqs. 2.39-2.42), the phononic density of modes
in Eq. 2.56, similar to the electronic quantities (Eqs. 2.39-2.42), the phononic density of modes
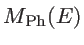 is calculated using the phononic bandstructures, where
is calculated using the phononic bandstructures, where
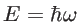 denotes the energy of a phonon with frequency
denotes the energy of a phonon with frequency 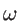 . In our calculations for phonon density of states
. In our calculations for phonon density of states
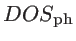 , we broadened the delta function by
, we broadened the delta function by
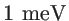 . This helps to numerically smoothen the DOS function, without affecting the thermal conductance calculations.
. This helps to numerically smoothen the DOS function, without affecting the thermal conductance calculations.
The FCM can also be effectively coupled to NEGF for the investigation of coherent
phonon transport in low dimensional systems. The NEGF method has been traditionally employed for electronic transport studies, but has been extended to phonon studies as well [54]. Here, the phononic device Green's function is obtained by
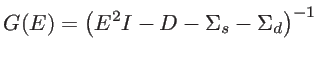 |
(2.57) |
where 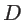 is device dynamic matrix and
is device dynamic matrix and
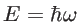 is the phonon energy [59]. Note that this is a Green's function of a classical wave equation, which is second order in time. Therefore, the square of the energy appears in Eq. 2.57. This is in contrast to the Schrodinger equation for quantum treatment of electrons which is first order in time, such that the eigen energy
is the phonon energy [59]. Note that this is a Green's function of a classical wave equation, which is second order in time. Therefore, the square of the energy appears in Eq. 2.57. This is in contrast to the Schrodinger equation for quantum treatment of electrons which is first order in time, such that the eigen energy 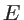 appears linearly in that case.
appears linearly in that case.
Finally, similar to the electron transport, the transmission probability of phonons through the rough channel can then be calculated using:
![$\displaystyle \overline{T}_{\mathrm{ph}}(E)=\mathrm{Trace}[\Gamma_{\mathrm{s}}G\Gamma_{\mathrm{d}}G^{\dagger}]$](img305.png) |
(2.58) |
Here, the phononic broadening and contact self-energy matrices are obtained in a similar way as the electronic ones (Eq. 2.51) with the substitutions
 and
and
 .
.



Next: 2.4.2 Boltzmann Transport Equation
Up: 2.4 Phonon Transport
Previous: 2.4 Phonon Transport
Contents
H. Karamitaheri: Thermal and Thermoelectric Properties of Nanostructures
![$\displaystyle I_q=\frac{1}{h}\int_{0}^{+\infty} \overline{T}_{\mathrm{ph}}(\ome...
...left [ n_{\mathrm{s}}(\omega)-n_{\mathrm{d}}(\omega) \right ] \ d(\hbar \omega)$](img292.png)
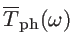 , the Bose-Einstein distribution function
, the Bose-Einstein distribution function ![$\displaystyle I_q=\frac{1}{h}\int_{0}^{+\infty} \overline{T}_{\mathrm{ph}}(\ome...
...left [ n_{\mathrm{s}}(\omega)-n_{\mathrm{d}}(\omega) \right ] \ d(\hbar \omega)$](img292.png)
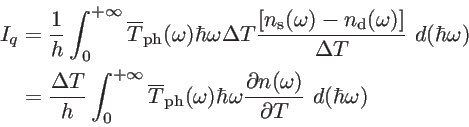
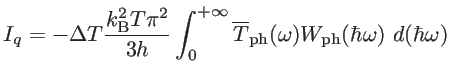
![\begin{displaymath}\begin{split}W_{\mathrm{ph}}(\hbar \omega)&=-\frac{3}{\pi^2}\...
...ar \omega}{2 k_{\mathrm{B}}T}\right ) \right ]^{-2} \end{split}\end{displaymath}](img295.png)
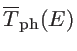 in Eq. 2.56, similar to the electronic quantities (Eqs. 2.39-2.42), the phononic density of modes
in Eq. 2.56, similar to the electronic quantities (Eqs. 2.39-2.42), the phononic density of modes
![]() is calculated using the phononic bandstructures, where
is calculated using the phononic bandstructures, where
![]() denotes the energy of a phonon with frequency
denotes the energy of a phonon with frequency ![]() . In our calculations for phonon density of states
. In our calculations for phonon density of states
![]() , we broadened the delta function by
, we broadened the delta function by
![]() . This helps to numerically smoothen the DOS function, without affecting the thermal conductance calculations.
. This helps to numerically smoothen the DOS function, without affecting the thermal conductance calculations.
![$\displaystyle \overline{T}_{\mathrm{ph}}(E)=\mathrm{Trace}[\Gamma_{\mathrm{s}}G\Gamma_{\mathrm{d}}G^{\dagger}]$](img305.png)