|

|
The Seebeck coefficient and power factor are sensitive to the details
of the density of states and the asymmetry between electrons and
holes [85,86]. The electronic band
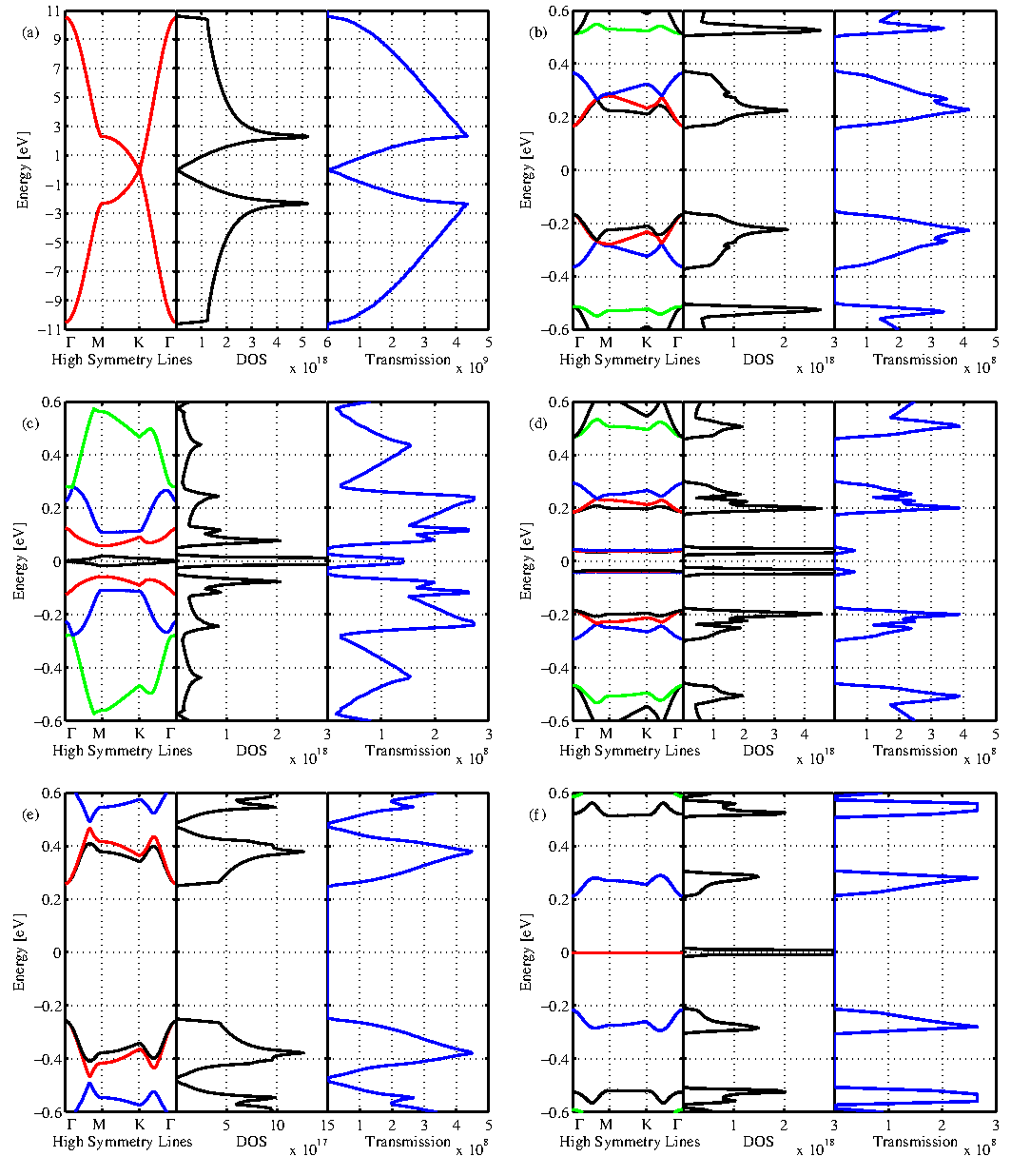
structures of GALs are calculated using a third nearest-neighbor tight-binding
method (Sec 2.1.1). By introducing the antidots in the graphene sheet, the zero
band-gap graphene can be converted into a narrow band-gap
semiconductor [26,27] (see Fig. 3.13). This
issue plays an important role in thermoelectric applications. In
contrast to pristine graphene, GALs have a beneficial
band-gap, so that one can suppress either the electron or the hole
current to obtain unipolar conduction. For example, by adjusting the
Fermi level near the conduction band the hole current will be
negligible. The electron-hole asymmetry with respect to the Fermi level
depends on the band-gap, on the sharp features of transmission, on the
width of the first conduction subband, and on the value of the
transmission. At room temperature, the width of the thermal broadening function
is about
![]() . Therefore, a band-gap around
. Therefore, a band-gap around
![]() and a first conduction subband width larger than
and a first conduction subband width larger than
![]() will be ideal for thermoelectric applications.
will be ideal for thermoelectric applications.
In RightTri(10,126), there are some localized midgap states, see
Fig. 3.13-f, as a result of sublattice-symmetry
breaking [84,87]. They have a zero group velocity and
can not contribute to the carrier transport. Although RightTri(10,126)
has the sharpest features in the transmission and its transport
band-gap is about
![]() , the width of the first conduction
subband of RightTri(10,126) is only
, the width of the first conduction
subband of RightTri(10,126) is only
![]() . As a result,
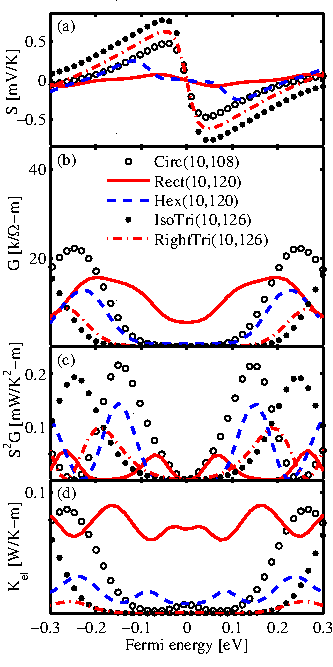
it has a high Seebeck coefficient and a low electrical conductance,
see Fig. 3.14. The first conduction subband of a
Rect(10,120) has a non-zero group velocity. Therefore, the
rectangular GAL is considered as a zero band-gap material and as a result, the
Seebeck coefficient will be small which is detrimental to
thermoelectric applications. In a Hex(10,120), the first conduction
and valence subbands are quasi-flat bands due to existence of some
edge carbon atoms which have only one nearest
neighbor [87]. As shown in Fig. 3.13-d, these bands
have a small group velocity and have a small contribution to electron
transport. As a result, the maximum value of the Seebeck coefficient of
Hex(10,120) is not very large and is located close to the band-edge of
the second conduction subband. On the other hand, the electrical
conductance peaks close to the second subband-edge. Therefore,
Hex(10,120) has the third highest power factor among the GALs with
different antidot shapes.
. As a result,
it has a high Seebeck coefficient and a low electrical conductance,
see Fig. 3.14. The first conduction subband of a
Rect(10,120) has a non-zero group velocity. Therefore, the
rectangular GAL is considered as a zero band-gap material and as a result, the
Seebeck coefficient will be small which is detrimental to
thermoelectric applications. In a Hex(10,120), the first conduction
and valence subbands are quasi-flat bands due to existence of some
edge carbon atoms which have only one nearest
neighbor [87]. As shown in Fig. 3.13-d, these bands
have a small group velocity and have a small contribution to electron
transport. As a result, the maximum value of the Seebeck coefficient of
Hex(10,120) is not very large and is located close to the band-edge of
the second conduction subband. On the other hand, the electrical
conductance peaks close to the second subband-edge. Therefore,
Hex(10,120) has the third highest power factor among the GALs with
different antidot shapes.
|
On the other hand, the band-gap and the first conduction subband width
of Circ(10,108) and IsoTri(10,126) are nearly
![]() and
and
![]() , respectively. They also have the highest
transmissions. Therefore, as shown in
Fig. 3.14, they are the best thermoelectric GALs in
terms of the power factor. Because of a sharp feature in the
transmission, Circ(10,108) has the highest power factor of the
GALs considered. In addition, as shown in Fig. 3.14-d the
electron contribution to the thermal conductance can be neglected in
comparison with the lattice thermal conductance (see
Table 3.2).
, respectively. They also have the highest
transmissions. Therefore, as shown in
Fig. 3.14, they are the best thermoelectric GALs in
terms of the power factor. Because of a sharp feature in the
transmission, Circ(10,108) has the highest power factor of the
GALs considered. In addition, as shown in Fig. 3.14-d the
electron contribution to the thermal conductance can be neglected in
comparison with the lattice thermal conductance (see
Table 3.2).