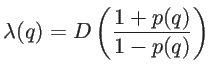 |
(5.8) |
We now examine the significance of phonon-boundary scattering at long wavelength, which is the scattering mechanism that dominates thermal transport. Strong phonon-boundary scattering is indeed the reason for increased thermoelectric performance of nanostructures and silicon nanowires in particular [20]. Boundary scattering reduces the phonon MFP and thus the thermal conductivity. The boundary scattering-limited MFP can be obtained from Eq. 5.2 as:
|
The term in the bracket of Eq. 5.8 is large for long wavelength phonons because the specularity parameter ![]() peaks at
peaks at ![]() as shown in the inset of Fig. 5.5. Long wavelength phonons have
as shown in the inset of Fig. 5.5. Long wavelength phonons have ![]() , which means that they undergo specular boundary scattering. In other words, waves of lengths larger than the average roughness features are not affected by the roughness and are more specularly reflected. Phonons of smaller wavelengths (larger
, which means that they undergo specular boundary scattering. In other words, waves of lengths larger than the average roughness features are not affected by the roughness and are more specularly reflected. Phonons of smaller wavelengths (larger ![]() ) scatter more diffusively, as the roughness feature sizes are of the
order of their wavelengths [139]. As we observed in Fig. 5.4, however, the heat transport in thinner nanowires is shifted towards the low-wavevector phonon states as the diameter is reduced. These states, however, are affected very weakly by boundary scattering due to their large
) scatter more diffusively, as the roughness feature sizes are of the
order of their wavelengths [139]. As we observed in Fig. 5.4, however, the heat transport in thinner nanowires is shifted towards the low-wavevector phonon states as the diameter is reduced. These states, however, are affected very weakly by boundary scattering due to their large ![]() , which makes the boundary overall more specular (although the thermal conductivity is still severely degraded due to the reduction in diameter).
, which makes the boundary overall more specular (although the thermal conductivity is still severely degraded due to the reduction in diameter).
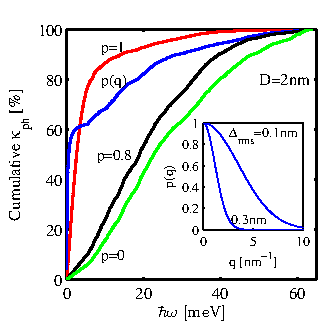
Figure 5.5 illustrates the importance of this wavevector-dependence of the specularity parameter ![]() on the cumulative thermal conductivity for the
on the cumulative thermal conductivity for the
![]() nanowire. The phonon-phonon scattering-limited result of Fig. 5.4 which corresponds to the fully specular case (
nanowire. The phonon-phonon scattering-limited result of Fig. 5.4 which corresponds to the fully specular case (![]() ), is also shown by the red line for reference. For fully diffusive boundaries (
), is also shown by the red line for reference. For fully diffusive boundaries (![]() for all frequencies), the thermal conductivity is almost equally distributed over the phonon energy (Fig. 5.5, green line). Note that here we use
for all frequencies), the thermal conductivity is almost equally distributed over the phonon energy (Fig. 5.5, green line). Note that here we use
![]() . A similar result is observed once a constant specularity parameter is used, i.e.
. A similar result is observed once a constant specularity parameter is used, i.e. ![]() (Fig. 5.5, black line), as it is assumed in several studies [123,136,140]. Interestingly, the distribution of the thermal conductivity over phonon energy for the fully diffusive (
(Fig. 5.5, black line), as it is assumed in several studies [123,136,140]. Interestingly, the distribution of the thermal conductivity over phonon energy for the fully diffusive (![]() ), and the almost specular (
), and the almost specular (![]() ) boundary conditions is very similar. On the other hand, the cumulative thermal conductivity trend is different when the
) boundary conditions is very similar. On the other hand, the cumulative thermal conductivity trend is different when the ![]() -dependent
-dependent ![]() is taken into account (blue line) and looks very much like the phonon-phonon scattering-limited case. The importance of the low frequency modes becomes even stronger (sharper rise of the cumulative conductivity at low frequencies compared to the phonon-phonon scattering case), in which case almost
is taken into account (blue line) and looks very much like the phonon-phonon scattering-limited case. The importance of the low frequency modes becomes even stronger (sharper rise of the cumulative conductivity at low frequencies compared to the phonon-phonon scattering case), in which case almost ![]() of the total thermal conductivity is carried by phonons of energies below
of the total thermal conductivity is carried by phonons of energies below
![]() . Above energies of
. Above energies of
![]() , where the boundaries become totally diffusive for all frequencies (see inset of Fig. 5.5), the thermal conductivity is distributed almost equally over the remaining phonon energies. We note that the phonon energy above which the thermal conductivity becomes fully diffusive (e.g.
, where the boundaries become totally diffusive for all frequencies (see inset of Fig. 5.5), the thermal conductivity is distributed almost equally over the remaining phonon energies. We note that the phonon energy above which the thermal conductivity becomes fully diffusive (e.g. ![]() becomes zero) is determined by the roughness amplitude. For smaller amplitudes, e.g.
becomes zero) is determined by the roughness amplitude. For smaller amplitudes, e.g.
![]() as shown in the inset of Fig. 5.5,
as shown in the inset of Fig. 5.5, ![]() indicates a stronger specular scattering behavior in a larger part of the phonon energy spectrum.
indicates a stronger specular scattering behavior in a larger part of the phonon energy spectrum.
|
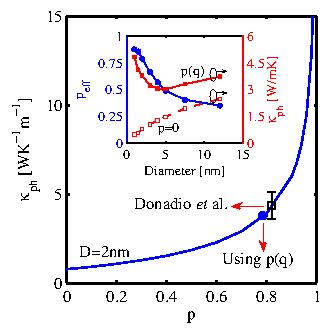
Therefore, for ultra-thin nanowires, it is not appropriate to use a constant specularity parameter for phonons of all wavevectors as is often assumed for thicker nanowires [123,141]. The underlying wavevector contributions to the thermal conductivity cannot be captured accurately, although one could adjust the specularity parameter to fit experimental measurements. This is illustrated in Fig. 5.6, which shows the thermal conductivity of the
![]() nanowire versus constant values of the specularity parameter (the same
nanowire versus constant values of the specularity parameter (the same ![]() for all wavevectors). The thermal conductivity remains low (below
for all wavevectors). The thermal conductivity remains low (below
![]() for a large range of
for a large range of ![]() , even up to
, even up to ![]() , and is smaller than the Umklapp scattering-limited conductivity by more than an order of magnitude. The blue dot indicates the thermal conductivity of the same nanowire, with the same roughness amplitude, using the wavevector dependent
, and is smaller than the Umklapp scattering-limited conductivity by more than an order of magnitude. The blue dot indicates the thermal conductivity of the same nanowire, with the same roughness amplitude, using the wavevector dependent ![]() as described by Eq. 5.3. In this case,
as described by Eq. 5.3. In this case,
![]() , which is also in good agreement with the result of MD simulations by Donadio et al. (black-square point) for the same nanowire [122]. In order for the two approaches (constant
, which is also in good agreement with the result of MD simulations by Donadio et al. (black-square point) for the same nanowire [122]. In order for the two approaches (constant ![]() versus
versus ![]() ) to provide the same value for the thermal conductivity, a constant specularity parameter of
) to provide the same value for the thermal conductivity, a constant specularity parameter of ![]() needs to be used. The large effective specularity parameter indeed illustrates that the phonon-boundary scattering is almost specular. This is a consequence of the increasing importance of the large wavelength phonons that scatter almost specularly on the nanowire boundary as the diameter is reduced. Indeed, if one extracts an effective constant specularity parameter, that provides the same value for the thermal conductivity as the wavevector-dependent
needs to be used. The large effective specularity parameter indeed illustrates that the phonon-boundary scattering is almost specular. This is a consequence of the increasing importance of the large wavelength phonons that scatter almost specularly on the nanowire boundary as the diameter is reduced. Indeed, if one extracts an effective constant specularity parameter, that provides the same value for the thermal conductivity as the wavevector-dependent ![]() , then this number will increase as the diameter is decreased. This is shown in the inset of Fig. 5.6 (left axis). The effective specularity parameter saturates around
, then this number will increase as the diameter is decreased. This is shown in the inset of Fig. 5.6 (left axis). The effective specularity parameter saturates around ![]() for larger nanowire diameters, which is close to the value usually assumed for larger nanowires. As the diameter is reduced to
for larger nanowire diameters, which is close to the value usually assumed for larger nanowires. As the diameter is reduced to
![]() , however, it increases even up to
, however, it increases even up to ![]() , a consequence of the dominant role of the long wavelength phonons.
, a consequence of the dominant role of the long wavelength phonons.
Figure 5.6, therefore, demonstrates the counter-intuitive result that for the same roughness, boundary scattering is overall more specular for ultra-thin nanowires than for thicker ones. The phonon-boundary scattering, however, is still dominant and causes thermal conductivity reduction from
![]() (phonon-phonon only as shown in Fig. 5.2), to
(phonon-phonon only as shown in Fig. 5.2), to
![]() . The degradation, though, originates from the influence of the diameter reduction on the MFP (see Eq. 5.8), and not from the diffusive nature of the boundary.
Interestingly, however, for diameters below
. The degradation, though, originates from the influence of the diameter reduction on the MFP (see Eq. 5.8), and not from the diffusive nature of the boundary.
Interestingly, however, for diameters below
![]() , the term in the bracket of Eq. 5.8 increases faster than the reduction in
, the term in the bracket of Eq. 5.8 increases faster than the reduction in ![]() . The MFP then starts to increase, the effect of phonon-boundary scattering is reduced, and the thermal conductivity increases. This is indicated in the inset of Fig. 5.6 (right axis), which shows that as the effective specularity
increases with decreasing diameter, the same happens to the thermal conductivity as well (solid-square red line). In contrast, a fully diffusive boundary with
. The MFP then starts to increase, the effect of phonon-boundary scattering is reduced, and the thermal conductivity increases. This is indicated in the inset of Fig. 5.6 (right axis), which shows that as the effective specularity
increases with decreasing diameter, the same happens to the thermal conductivity as well (solid-square red line). In contrast, a fully diffusive boundary with ![]() as one would assume for such thin nanowire, results to a monotonic decrease in the conductivity as the diameter is reduced (dashed-square red line).
as one would assume for such thin nanowire, results to a monotonic decrease in the conductivity as the diameter is reduced (dashed-square red line).