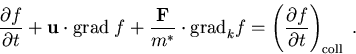2.1 Die Transportgleichung  

Grundlage für die in der Bauteilsimulation abgeleiteten Differentialgleichungen ist die BOLTZMANN-Transportgleichung. Ausgehend von dieser Gleichung werden die Bauteilgleichungen der unterschiedlichen Modellsysteme hergeleitet [6,7]. Die Gleichung lautet in differentieller Form

$$\begin{eqnarray} \frac{\partial f}{\partial t} + \vec{u} \cdot \mathrm{grad}\; f... ...= \left(\frac{\partial f}{\partial t}\right)_{\mathrm{coll}}\; . \end{eqnarray}$$ (2.1)

Die Transportgleichung beschreibt das Verhalten von Teilchensystemen in Anwesenheit äußerer Kraftfelder. Sie ist eine klassische Kontinuumsgleichung, Teilcheneffekte oder Quanteneffekte werden nicht berücksichtigt. Die Gleichung ist die bestimmende Gleichung für die Verteilungsfunktion $f(t,\vec{r},\vec{k})$, welche sich entsprechend den äußeren Kraftfeldern einstellt.

Der erste Term der linken Seite von (2.1) beschreibt die Änderung der Verteilungsfunktion mit der Zeit. Der zweite Summand wird als Diffusionsterm bezeichnet und stellt die örtliche Abhängigkeit der Verteilungsfunktion dar. Er hängt von der lokalen Größe der Teilchengeschwindigkeit $\vec{u}$ ab. Der dritte Term der linken Seite wird als Feldterm bezeichnet und beschreibt z. B. die geschwindigkeitsabhängige Veränderung der Verteilungsfunktion aufgrund eines äußeren Feldes $\vec{E}$.

Die rechte Seite schließlich wird als Stoßterm bezeichnet. Sie beschreibt die Veränderung der Verteilungsfunktion aufgrund elastischer und inelastischer Stöße.

Den Unterschied zwischen dem Diffusionsterm und dem Feldterm kann man folgendermaßen interpretieren. Der Diffusionsterm beschreibt ein thermodynamisches System aufgrund des phänomenologischen Verhaltens. Mit Hilfe der Verteilungsfunktion werden effektive Kräfte berechnet, die auf das Gesamtsystem der Teilchen wirken. Diese Kräfte sind mikroskopisch nicht erklärbar. Sie sind nur im Rahmen der statistischen Mechanik in einem Vielteilchensystem erfaßbar. Die aus (2.1) berechneten Diffusionsteilkräfte auf das thermische System sind im Fall der Halbleitergleichungen proportional zum Gradienten der Temperatur und zum Gradienten der Ladungsträgerkonzentration.

In einem Teilchensystem mit konstanter Temperatur, aber unterschiedlicher örtlicher Ladungsträgerkonzentration wird sich das System aufgrund statistischer Stöße so relaxieren, daß sich eine räumlich konstante Konzentration einstellt. Die maximale Geschwindigkeit, mit der der Relaxationsvorgang stattfinden kann, ist durch die örtlich konstante, thermische Geschwindigkeit begrenzt. Dabei wird die Diffusion der Teilchen zu Gebieten mit niedrigerer Konzentration durch eine makroskopische, effektive Kraft beschrieben, die proportional zum Gradienten der Teilchenkonzentration ist.

In einem System mit konstanter Teilchenkonzentration, aber unterschiedlicher lokaler Teilchentemperatur, werden heiße Teilchen aufgrund der thermischen Bewegung in Gebiete diffundieren, wo sich kältere Teilchen aufhalten. Dort nimmt ihre thermische Geschwindigkeit durch inelastische Stöße ab, worauf das Verlassen des ,,kalten`` Gebietes erschwert wird. Die Diffusion der Teilchen zu Gebieten mit niedrigerer Temperatur wird durch eine makroskopische, effektive Kraft beschrieben, die proportional zum Gradienten der Teilchentemperatur ist.

Im Gegensatz zum Diffusionsterm wird der Driftterm von (2.1) mit Hilfe einer mikroskopischen Kraft $\vec{F}$auf ein Teilchen bestimmt. Elektrostatische oder magnetische Kräfte sind typische Beispiele dafür. Um das örtliche Verhalten des Teilchensystems beschreiben zu können, ist jedoch gleichfalls eine Integration über den Geschwindigkeitsraum notwendig.

Eine Lösung der Transportgleichung stellt die Stromgleichung dar, die den Teilchenfluß im Bauteil beschreibt. Hat man die Partialkräfte der Diffusions- und Driftterme von (2.1) berechnet, so kann man formal die Kraft auf ein Teilchen als Summe der makroskopischen und mikroskopischen Kräfte beschreiben, obwohl vom physikalischen Standpunkt aus nur mikroskopische Kräfte auf das Teilchen wirken. Diese resultierende Gesamtkraft ist entscheidend für das gesamte Bauteilverhalten. Sie bestimmt letztlich die lokalen Stromdichten, sowie die Konzentration der Ladungsträger.

Die in der Bauteilsimulation verwendeten Differentialgleichungen werden mit Hilfe der Momentenmethode aus der BOLTZMANN-Transportgleichung gewonnen. Dabei entspricht der lokale, gewichtete Mittelwert der Momentenfunktion $\Phi$ im Geschwindigkeitsraum einem Erwartungswert der entsprechenden Größe an einem Ortspunkt. Allgemein ist $\Phi$ eine Größe von $\Phi(t,\vec{r},\vec{k})$. Das Moment ist definiert als

$$\begin{eqnarray} \Phi(t,\vec{r})=\langle \Phi(t,\vec{r},\vec{k}) \rangle = \frac... ...ox{d}^3 k}{\int_{V_k} f(t,\vec{r},\vec{k})\cdot \mbox{d}^3 k}\; . \end{eqnarray}$$ (2.2)

Die Integration der Verteilungsfunktion über den $\vec{k}$-Raum ergibt die orts- und zeitabhängige Teilchendichte c

$$\begin{eqnarray} c(t,\vec{r})= \int_{V_k} f(t,\vec{r},\vec{k})\cdot \mbox{d}^3 k\; . \end{eqnarray}$$ (2.3)

Die Integration über den $\vec{k}$-Raum entspricht einer Integration im Impulsraum. Klassisch kann man das mit einer Integration im Geschwindigkeitsraum gleichsetzen, wenn man im Fall von Halbleitern eine konstante, skalare, effektive Teilchenmasse $m^{\ast}$ annimmt, die unabhängig von der Energie E ist. Im allgemeinen Fall berechnet sich die reziproke effektive Masse eines Kristallelektrons, welches BLOCH-Wellen als Eigenfunktionen annimmt, zu

$$\begin{eqnarray} \frac{1}{m^\ast}= \frac{1}{\hbar^2}\cdot \frac{\partial^2 E(\vec{k})}{\partial k_i\partial k_j}\; . \end{eqnarray}$$ (2.4)

Die Größe $E(\vec{k})$ in (2.4) bezeichnet man als Dispersionsrelation. Sie gibt den Zusammenhang zwischen der Energie und dem Wellenvektor k an. Bei einem isotropen Material, d.h. es gibt keine Raumvorzugsrichtungen, ist 2.4 für eine konstante Teilchenmasse genau dann erfüllt, wenn man für die Dispersionsrelation einen parabolischen Bandkantenverlauf der Form

$$\begin{eqnarray} E(k) = E(k_0) + \frac{\hbar^2 \cdot(k-k_0)^2}{2\cdot m^\ast}\; . \end{eqnarray}$$ (2.5)

animmt. Dabei besitzt E(k) an der Stelle k=k₀ ein Extremum.

Die Annahme einer energieunabhängigen effektiven Masse ist in den heutigen Bauteilsimulatoren üblich, obwohl diese Annahme nur bei kleinen Energien exakt zutrifft. Im Gegensatz dazu wird die Teilchenmasse jedoch oft gittertemperaturabhängig modelliert.

Die Integration über den $\vec{k}$-Raum ist ebenfalls nur klassisch möglich, da quantenmechanisch nur diskrete Zustände erlaubt sind. Der Abstand der diskreten Energieniveaus ist umso größer, je niedriger die betrachteten Energien der Niveaus sind. Quantenmechanisch korrekt müßte man daher die Integration über den $\vec{k}$-Raum durch eine Summation über die erlaubten Zustände ersetzen. In dieser Arbeit wird jedoch weiterhin die Notation der kontinuierlichen Schreibweise verwendet.

Multipliziert man (2.1) mit $\Phi$ und integriert man über den $\vec{k}$-Raum, so erhält man

$$\begin{eqnarray} \frac{\partial}{\partial{t}}\int_{V_k} \Phi \cdot f \cdot \mbox... ...partial t}\right)_{\mathrm{coll}}\!\!\!\!\cdot \!\mbox{d}^3 k\; , \end{eqnarray}$$ (2.6)

wobei man für den dritten Summand von (2.1) folgende Umformung verwendet hat

$$\begin{eqnarray} \int_{V_k} \Phi \cdot \frac{\vec{F}}{m^\ast}\mathrm{div}_{k}f\c... ...t \int_{V_k} f \cdot \mathrm{grad}_{k} \Phi\cdot \mbox{d}^3 k\; . \end{eqnarray}$$ (2.7)

Man kann zeigen, daß der erste Term der rechten Seite von (2.6) verschwindet, weil die Verteilungsfunktion f bei großen Werten von $\vec{k}$ gegen Null strebt (Satz von GAUß).

Letztlich erhält man unter Berücksichtigung von (2.3) die Transportgleichung für beliebige Momente $\Phi$[43]

$$\begin{eqnarray} \frac{\partial(c\cdot \langle \Phi\rangle)}{\partial t}+\mathrm... ...(\frac{\partial f}{\partial t}\right)_{\mathrm{coll}})\rangle\; . \end{eqnarray}$$ (2.8)

Mit Hilfe von (2.8) werden in der Folge die Differentialgleichungen des Drift-Diffusionsmodells und des hydrodynamischenModells hergeleitet.