previous up next contents Previous: 9.1 Quantum Electron-Phonon Scattering Up: 9. Stochastic Methods and Next: 9.3 A Scattering Interpretation

9.2 Boltzmann-Type Scattering

Considered is the Wigner equation which accounts for the nondissipative part of the transport via the coherent free term and the Wigner potential $ V_{\mathrm{w}}$ and for dissipation processes via the Boltzmann collision operator $ B$. In the Monte Carlo simulation all three dimensions of the momentum space can be considered.

In contrast the finite difference methods consider the momentum space only as one-dimensional. Dissipation is only included in a relaxation time approximation [SHMS98].

For one-dimensional devices the equation reads:

\begin{gather*}\begin{split}&\left(\frac{\partial}{\partial t} +\frac{\hbar k_x}... ...k_x}'-{ k_x})f_{\mathrm{w}}(x,k_x',{\bf k}_{yz},t) . \end{split}\end{gather*} (9.1)

The Boltzmann collision operator is defined by the scattering rate $ S$

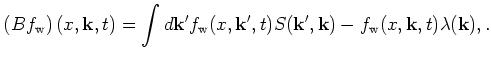$\displaystyle \left(Bf_{\mathrm{w}}\right)(x,{\bf k},t) = \int d {\bf k}' f_{\m... ...\bf k}',t)S({\bf k}',{\bf k}) - f_{\mathrm{w}}(x,{\bf k},t)\lambda ({\bf k}), .$    

$ S({\bf k}',{\bf k})$ is the probability density per unit time for scattering from state $ (x,{\bf k}')$ to state $ (x,{\bf k})$. $ S$ is a cumulative quantity which accounts for different scattering sources such as phonons and impurities. The total out-scattering rate $ \lambda$ is defined by the integral over all after-scattering states as

$\displaystyle \lambda({\bf k})=\int S({\bf k}, {\bf k}') d{\bf k}' .$ (9.2)

We stress that the Boltzmann scattering operator is a superoperator and cannot be written as an ordinary commutator. Technically this is the way in which proper quantum mechanics - which is time-reversible - is extended. As the Wigner formalism is naturally a superoperator formalism this is more easily achieved in the Wigner picture [Roy91]. The superoperator formalism was favored by Prigogine [GP79] as a framework for time-irreversible quantum mechanics.

previous up next contents Previous: 9.1 Quantum Electron-Phonon Scattering Up: 9. Stochastic Methods and Next: 9.3 A Scattering Interpretation

R. Kosik: Numerical Challenges on the Road to NanoTCAD