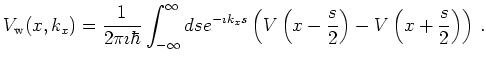previous up next contents Previous: 9.2 Boltzmann-Type Scattering Up: 9. Stochastic Methods and Next: 9.4 The Negative Sign

9.3 A Scattering Interpretation of the Potential Operator

Both quantum mechanics and stochastic process theory deal with dynamical systems which can be predicted only probabilistically. Efforts to reformulate quantum mechanics in terms of the theory of stochastic processes are legion [Nel66], [SS98], [GHT79], [MR88].

How to account for the complete potential term is the main concern of the stochastic particle approach. Here we present a formulation of potential scattering as a real stochastic process which retains the basic features of the weighted Single Particle MC method [KNS01]. This approach was already tried in [NDB+97]. An approach close to ours is given in [SM93]. There also exist some similarities with the phase-space path integral approach [Mar91].

The Wigner potential is defined by the Fourier transform

$\displaystyle V_{\mathrm{w}}(x,{k_x})= \frac{1}{2\pi\imath\hbar} \int_{-\infty}... ... V\left(x - \frac{{ s}}{2}\right)- V\left(x + \frac{{ s}}{2}\right)\right) .$ (9.3)

Formally the Wigner potential operator is similar to a Boltzmann inscattering operator. However, it is seen from the definition that the Wigner potential is odd in $ k_x$. Hence the inscattering rates can become negative. Negative inscattering can be interpreted as annihilation of particles, positive inscattering is interpreted as creation of particles. The sum over the inscattering probabilities is zero (as $ V_{\mathrm{w}}$ is odd in $ k$) and the process itself conserves mass. Negative inscattering may result in negative values for $ f_{\mathrm{w}}$, which defies a classical stochastic interpretation but is in accordance with the general properties of the Wigner function which can obtain negative values.

In a Monte Carlo view the Wigner potential $ V_{\mathrm{w}}$ is seen as an indefinite measure $ V_{\mathrm{w}} = V_{\mathrm{w}}^+ - V_{\mathrm{w}}^-$, where $ V_{\mathrm{w}}^+$ and $ V_{\mathrm{w}}^-$ are positive. For nonzero bias the Wigner potential $ V_{\mathrm{w}}$ has a $ \delta$-singularity for $ k = 0$. This singularity can be removed by introducing a constant electric field $ E$ in the Monte Carlo simulation. A numerical integral evaluation naturally splits into two separate ensembles with weight $ V_{\mathrm{w}}^+$ and $ V_{\mathrm{w}}^-$.

This splitting suggests to rewrite the Wigner equation in terms of two positive species $ f^+, f^-$ (particles and ``antiparticles") where negative inscattering is interpreted as creation of an antiparticle.

In this interpretation the Wigner equation becomes a system of equations:

\begin{gather*}\begin{split}& \frac{\partial f^+}{\partial t} = \int f^+(x,k',t)... ...+ \int f^+(x,k',t) V_{\mathrm{w}}^-(x,k-k')dk' + \cdots \end{split}\end{gather*} (9.4)

Here we have not written down the terms from the free operator and from Boltzmann scattering. Subtracting the second from the first equation gives the original Wigner equation for the quantity $ f_{\mathrm{w}} = f^+ - f^-$.

Regarding the mathematical equivalence of quantum mechanics and real stochastic processes we note that a quantization constraint has to be imposed on the stochastic process as not every function $ f$ represents a quantum distribution. We know of no stochastic interpretation for this constraint.

previous up next contents Previous: 9.2 Boltzmann-Type Scattering Up: 9. Stochastic Methods and Next: 9.4 The Negative Sign

R. Kosik: Numerical Challenges on the Road to NanoTCAD