previous up next contents Previous: 2.2.1 Macroscopic Observables Up: 2.2.1 Macroscopic Observables Next: 2.2.1.2 Physical Quantities

2.2.1.1 Sets of Moments

The description of the distribution function $ f$ by a set of moments eliminates the $ k$-coordinates at the expense of information loss concerning the details of the distribution function, as the common simplification is to investigate only a few moments of the distribution function.

In the parabolic case the energy $ \varepsilon$ is

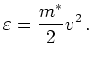$\displaystyle \varepsilon = \frac{m^*}{2} v^2 .$ (2.20)

In this special case we can choose the observables to be polynomials in $ v$.

We set

$\displaystyle u = v^2 = v_3^2 + v_r^2.$ (2.21)

and we define the set of velocity observables:

$\displaystyle O = \{O_0, O_1, O_2, O_3, O_4, O_5, O_6\} = \{1,v_3,u,v_3 u,u^2,v_3u^2,u^3\} .$ (2.22)

The moments derived from these observables are denoted by $ M_i$. This set of moments naturally corresponds to the use of a ``shifted'' distribution function (diffusion approximation) as defined in Equation 2.17.

For the non-parabolic case the following set of observables is more appropriate and is used in [GJK+04]:

$\displaystyle P = \{P_0, P_1, P_2, P_3, P_4, P_5, P_6\} = \{1, v_3, \varepsilon, v_3 \varepsilon, \varepsilon^2, v_3 \varepsilon^2, \varepsilon^3\}$ (2.23)

We define the ``energy'' moments as

$\displaystyle V_{2i} = \langle \varepsilon^i \rangle$ (2.24)

and the fluxes

$\displaystyle V_{2i+1} = \langle v_3 \varepsilon^i \rangle.$ (2.25)

In the parabolic band case the energy and the velocity set of moments are equivalent descriptions. In this case the quotient between the velocity moments and the energy moments depends on $ i=0,1,2$. We have

$\displaystyle V_{2i+k} = \bigl( \frac{m^*}{2}\bigr)^i M_{2i+k} , \qquad M_{2i+k}= V_{2i+k} \bigl( \frac{2}{m^*} \bigr)^i ,$ (2.26)

where $ k=0,1$.

previous up next contents Previous: 2.2.1 Macroscopic Observables Up: 2.2.1 Macroscopic Observables Next: 2.2.1.2 Physical Quantities

R. Kosik: Numerical Challenges on the Road to NanoTCAD