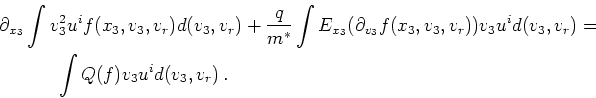 |
(2.35) |
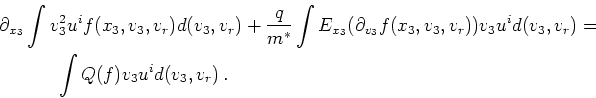 |
(2.35) |
For the first term we note that by the assumption of isotropy of the symmetric part we have
By using partial integration on the second term we obtain
| (2.37) |
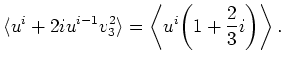 |
(2.38) |
In summary we get the following set of equations: For ![]() and
and
![]() :
:
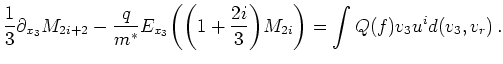 |
(2.39) |
The derivation does not need the full isotropy condition for its validity. Instead, we only need two reduction conditions:
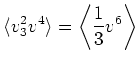 |
(2.41) |
| (2.42) |
So by using the isotropy condition we can eliminate the
moment
![]() .
For the validity of Equation 2.36 the isotropy
assumption is a sufficient, but not a
necessary condition. A simple counter example is
a function of the form
.
For the validity of Equation 2.36 the isotropy
assumption is a sufficient, but not a
necessary condition. A simple counter example is
a function of the form
![]() .
However, this form does not fulfill cylindrical
symmetry. Examples which fulfill cylindrical symmetry
can be constructed too, but one has to consider
multivariate polynomials up to sixth order for a proof.
.
However, this form does not fulfill cylindrical
symmetry. Examples which fulfill cylindrical symmetry
can be constructed too, but one has to consider
multivariate polynomials up to sixth order for a proof.
![]()
![]()
![]()
![]() Previous: 2.2.2.1 Even Moments
Up: 2.2.2 Hierarchy of Moment
Next: 2.2.2.3 Non-Parabolicity Corrections
Previous: 2.2.2.1 Even Moments
Up: 2.2.2 Hierarchy of Moment
Next: 2.2.2.3 Non-Parabolicity Corrections