In the simplest case the relaxation times
![]() are often modeled as constants.
are often modeled as constants.
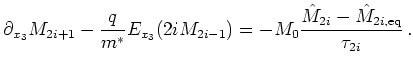 |
(2.53) |
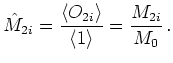 |
(2.54) |
For the even moments
the relaxation time approximation implies
that the perturbed moments of the distribution
function will relax exponentially to the equilibrium function
with time constant ![]() when the perturbing field is removed.
In this case we
relax the normalized quantities
when the perturbing field is removed.
In this case we
relax the normalized quantities
![]() to the values from a cold Maxwellian.
to the values from a cold Maxwellian.
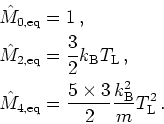 |
(2.55) |
Variants in the specification of
the relaxation time approximation are possible.
For the higher
order moments relaxation to values from a hot Maxwellian
with local temperature ![]() is a valid alternative.
is a valid alternative.
Often the relaxation time is modeled as depending on the
normalized
![]() , that is, local temperature.
For a comparison with Monte Carlo results the constant relaxation
time approximation can be too simplistic. A better
approximation is to tabulate it as a function of temperature
and doping extracted from bulk Monte Carlo simulations as
discussed in Section 2.3.4.
, that is, local temperature.
For a comparison with Monte Carlo results the constant relaxation
time approximation can be too simplistic. A better
approximation is to tabulate it as a function of temperature
and doping extracted from bulk Monte Carlo simulations as
discussed in Section 2.3.4.
The modeling of production terms by relaxation type models leads to inconsistencies with the Onsager reciprocity relations as stressed in [ARR00].
![]()
![]()
![]()
![]() Previous: 2.3 Closure Relations for
Up: 2.3 Closure Relations for
Next: 2.3.2 Odd Moments: Mobilities
Previous: 2.3 Closure Relations for
Up: 2.3 Closure Relations for
Next: 2.3.2 Odd Moments: Mobilities