

 Previous: 2.3.1 Even Moments: Relaxation
Up: 2.3 Closure Relations for
Next: 2.3.3 Analytical Mobility and
Previous: 2.3.1 Even Moments: Relaxation
Up: 2.3 Closure Relations for
Next: 2.3.3 Analytical Mobility and
As the odd equilibrium values vanish, the macroscopic
relaxation time approximation simplifies.
To approximate the odd scattering terms we introduce the
mobilities [GJK+04]
in the odd equations.
By setting
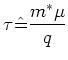 |
(2.56) |
we get a formal correspondence between relaxation times
and mobilities for parabolic bands. If 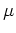 and
and 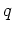 have the same sign, then
have the same sign, then 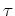 is positive.
is positive.
With this correspondence we get:
One possibility to model 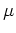 is as a function depending
on the the local temperature
is as a function depending
on the the local temperature
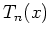 .
Hence the
equations depend in a nonlinear way on
.
Hence the
equations depend in a nonlinear way on 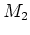 and
and  .
Information about the scattering term can be encoded
into a fitting
ansatz for the mobilities, for example in the
form
.
Information about the scattering term can be encoded
into a fitting
ansatz for the mobilities, for example in the
form
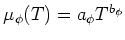 with fitting parameters
with fitting parameters
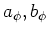 .
.
Alternatively, we can approximate the mobilities as
functions of temperature and doping using results from
bulk Monte Carlo simulations, see Section 2.3.4.


 Previous: 2.3.1 Even Moments: Relaxation
Up: 2.3 Closure Relations for
Next: 2.3.3 Analytical Mobility and
Previous: 2.3.1 Even Moments: Relaxation
Up: 2.3 Closure Relations for
Next: 2.3.3 Analytical Mobility and
R. Kosik: Numerical Challenges on the Road to NanoTCAD
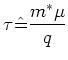
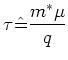
![]()
![]()
![]()
![]() Previous: 2.3.1 Even Moments: Relaxation
Up: 2.3 Closure Relations for
Next: 2.3.3 Analytical Mobility and
Previous: 2.3.1 Even Moments: Relaxation
Up: 2.3 Closure Relations for
Next: 2.3.3 Analytical Mobility and