previous up next contents Previous: 2.3.4 Consistency with Bulk Up: 2.3 Closure Relations for Next: 3. Highest Order Moment


2.3.5 Hierarchy of Equations

Using the mobility closure given by Equation 2.57 the fluxes can be eliminated. The system of first order moment equations then becomes a system of second order equations in the even moments.

With the relaxation time approximation the general equation for $ M_{2i}$ is of the following form:

$\displaystyle \partial_{x_3} M_{2i+1}(M_{2i+2},M_{2i}) - \frac{q}{m^{*}} E_{x_3... ..._{2i-2})) = -M_0 \frac{\hat{M}_{2i} - \hat{M}_{2i,\mathrm{eq}}}{\tau_{2i}(T_n)}$ (2.73)

Using the explicit expression for $ M_{2i+1}$

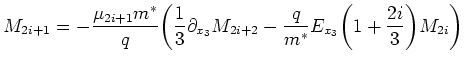$\displaystyle M_{2i+1} = - \frac{\mu_{2i+1} m^{*}}{q} \bigg( \frac{1}{3} \parti... ..._3} M_{2i+2} - \frac{q}{m^{*}} E_{x_3} \bigg(1 + \frac{2i}{3}\bigg)M_{2i}\bigg)$ (2.74)

we see that $ M_{2i+2}$ enters Equation 2.74 only through the term

$\displaystyle - \frac{1}{3} \partial_{x_3} \frac{\mu_{2i+1}(T_n) m^{*}}{q} \partial_{x_3} M_{2i+2} .$ (2.75)

This is the only second order term in Equation 2.74 and can be interpreted as a diffusion operator. The general equation for the $ M_{2i}$ equation can be supplemented with Dirichlet boundary conditions for $ M_{2i+2}$.

Besides $ M_{2i}$ the moments which enter in the equation for $ M_{2i}$ are $ M_{2i+2}$ and $ M_{2i-2}$. In addition we need $ M_0$ for the relaxation term. Furthermore relaxation times and mobilities depend on $ T_n$, which needs $ M_2$ (and $ M_0$) for its calculation.

Equation 2.74 gives an infinite hierarchy of equations. If $ M_0$ is fixed, we get the self-consistent electrical field from the Poisson equation. Then we can calculate $ M_2$ by solving the linear Equation 2.74 (with $ 2i=0$) for $ M_2$. For order $ 2i=0$ this is a nonlinear equation due to the dependence of $ \mu_1$ on $ M_0$ and $ M_2$ via the temperature.

In an infinite chain we then can solve linear equations with linear operator 2.76 to get $ M_4$, $ M_6$, and so on. The linearity is due to the exclusive dependence of $ \mu$ and $ \tau$ on $ M_0$ and $ M_2$ via the temperature. We also see that the infinite hierarchy has a solution for arbitrary chosen $ M_0$. This is a weakness of the model, the infinite hierarchy represents an underdetermined system of equations and is not equivalent to the full Boltzmann equation. The infinite system lacks a closure condition or constraint which picks out the ``one'' solution. In Section 3.2 we propose to apply the maximum entropy principle for this purpose.

As the infinite hierarchy is not equivalent to the Boltzmann equation it is reasonable to truncate the series at a low order $ 2i$. We then have to impose an additional equation for the highest occurring moment with order $ 2i+2$, to get an equal number of equations and unknowns. This closure condition is the topic of the next chapter.

previous up next contents Previous: 2.3.4 Consistency with Bulk Up: 2.3 Closure Relations for Next: 3. Highest Order Moment

R. Kosik: Numerical Challenges on the Road to NanoTCAD