previous up next contents Previous: 6.1.2 Hydrodynamical Formulation Up: 6.1 Quantum Mechanics in Next: 6.2 Quantum Mechanics in

6.1.3 The Riccati and Prüfer Equation

The Riccati equation was used in [Bit00] as a numerically more suitable variant of the hydrodynamical formulation.

Set

$\displaystyle z = \ln \psi .$ (6.28)

With this the stationary Schrödinger equation

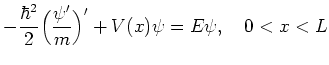$\displaystyle - \frac{\hbar^2}{2} \Bigl(\frac{\psi'}{m}\Bigr)' + V(x) \psi = E \psi,\quad 0 < x < L$    

becomes

$\displaystyle \frac{1}{m} \left( \frac{z'}{m} \right)' + \left( \frac{z'}{m} \right)^2 = 2 (V(x) - E) \frac{1}{m \hbar^2} .$ (6.29)

By the substitution

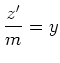$\displaystyle \frac{z'}{m} = y$ (6.30)

it reduces to a nonlinear first order equation. For constant mass $ m$ and $ z' = u$ we get

$\displaystyle u'(x) + {u(x)}^2 = 2 (V(x) - E) \frac{m}{\hbar^2}$ (6.31)

This type of equation is known as Riccati equation [MR96]. The Riccati equation plays an important role in control theory and has a rich theory of its own. Separation of Equation 6.30 into real and imaginary part recovers the hydrodynamical equation for the phase $ S$ as equation for the imaginary part of $ z$.

Another alternative formulation of the Schrödinger equation, which is closely related to the Riccati equation, is the Prüfer equation. The Prüfer transformation is a useful tool in the qualitative theory of second order Sturm-Liouville differential equations [BD01]. In the case of the Schrödinger equation with constant mass $ m$ it is introduced in the following way: Define complex quantities $ q,p$

$\displaystyle q =$ $\displaystyle \psi $ (6.32)
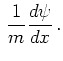$\displaystyle p =$ $\displaystyle \frac{1}{m} \frac{d \psi}{dx} .$ (6.33)

Introducing the transformation

$\displaystyle q$ $\displaystyle = r \cos(\alpha) ,$ (6.34)
$\displaystyle p$ $\displaystyle = r \sin (\alpha) ,$ (6.35)

with complex $ r$, and $ \alpha$ we get from the Schrödinger equation and from the defining equation for $ p$ (6.34)

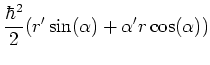$\displaystyle \frac{\hbar^2}{2} (r' \sin(\alpha) + \alpha' r \cos(\alpha))$ $\displaystyle = (E - V(x))r \cos(\alpha)$ (6.36)
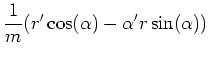$\displaystyle \frac{1}{m} (r' \cos(\alpha) - \alpha' r \sin(\alpha))$ $\displaystyle = r \sin (\alpha) .$ (6.37)

Respective multiplication of these equations with $ -\sin(\alpha)$ and $ \cos(\alpha)$ and adding the resulting equations yields (after elimination of $ r$):

$\displaystyle \alpha' = \frac{2 m}{\hbar^2}(V(x) - E) \cos^2(\alpha) - \sin^2(\alpha) .$ (6.38)

So the equation for the angular variable separates. For $ r$ we get:

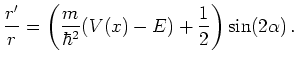$\displaystyle \frac{r'}{r} = \bigg( \frac{m}{\hbar^2}(V(x) - E) + \frac{1}{2}\bigg) \sin(2\alpha) .$ (6.39)

The link to the original Riccati idea is immediate. If $ \alpha$ is a solution to the Prüfer equation, then $ u = \tan(\alpha)$ is a solution to the Riccati Equation 6.32. The advantage of the Prüfer equation (6.39) over the traditional Riccati equation is that it can be solved for arbitrary $ \alpha$ without leading to singularities, as is the case with nodes ( $ \psi(x) = 0$) in the Riccati equation. The Schrödinger, Riccati and Prüfer equation will be investigated numerically in Section 7.1.3.

previous up next contents Previous: 6.1.2 Hydrodynamical Formulation Up: 6.1 Quantum Mechanics in Next: 6.2 Quantum Mechanics in

R. Kosik: Numerical Challenges on the Road to NanoTCAD