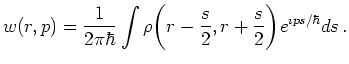 |
(6.40) |
Among the several transforms of the wave function or in general of the density operator, that provide a phase space view of the quantum state, the Wigner function is the one that has found more applications, mainly in statistical mechanics, but also in quantum chemistry, molecular dynamics, scattering theory, or quantum optics.
The Wigner function is (up to a constant factor) the Weyl transform of the quantum-mechanical density operator. For a particle in one dimension it takes the form
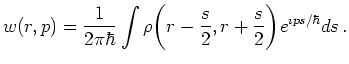 |
(6.40) |
Here
![]() denotes the von Neumann density function, i.e.,
denotes the von Neumann density function, i.e.,
| (6.41) |
This transformation can be conveniently split into two steps.
For this we define:
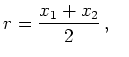 |
(6.42) |
We call ![]() the center of mass coordinate and
the center of mass coordinate and
![]() the distance coordinate. These names
should not be physically misleading as the von Neumann equation
does not describe a two-particle problem but quantum
correlations.
the distance coordinate. These names
should not be physically misleading as the von Neumann equation
does not describe a two-particle problem but quantum
correlations.
The inverse relation is
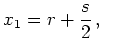 |
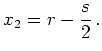 |
(6.43) |
Calculation of the Wigner distribution involves as a first step a
change to new
coordinates ![]() and
and ![]() .
This gives
.
This gives
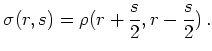 |
(6.44) |
In a second step this is followed
by a Fourier transformation with respect to ![]() .
.
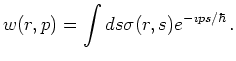 |
(6.45) |
An inverse Fourier transform gives the com distribution from the Wigner distribution:
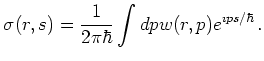 |
(6.46) |
Instead of the momentum coordinate ![]() it is possible to introduce
the wave vector
it is possible to introduce
the wave vector
![]() which eliminates
which eliminates ![]() from the
transformation:
from the
transformation:
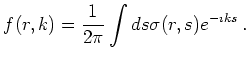 |
(6.47) |
Note that as ![]() is self-adjoint,
is self-adjoint,
So the Wigner distribution is real. However, in contrast to its classical analogon it can assume negative values. As position and momentum operators do not commute and hence cannot be measured together, this does not present an inconsistency.
The Wigner distribution possesses an important ![]() -
-![]() duality
given by the alternative definition [FJP03]
duality
given by the alternative definition [FJP03]
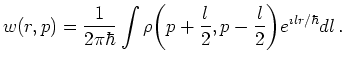 |
(6.48) |
![]()
![]()
![]()
![]() Previous: 6.2.1 Phase Space Distribution
Up: 6.2 Quantum Mechanics in
Next: 6.2.3 Operator-Theoretic Structure
Previous: 6.2.1 Phase Space Distribution
Up: 6.2 Quantum Mechanics in
Next: 6.2.3 Operator-Theoretic Structure