For operators which are functions of coordinates or momenta
only, such as ![]() or
or ![]() , the Weyl transform agrees with
the classical function corresponding to
, the Weyl transform agrees with
the classical function corresponding to ![]() . This can not be the
case in general, as is clear from the non-commutativity of
the operator product. For example the Weyl transform of
. This can not be the
case in general, as is clear from the non-commutativity of
the operator product. For example the Weyl transform of ![]() is
is
![]() .
.
The crucial question is: what does the operator product look like in phase space? This question was answered by Moyal in [Moy49] by introduction of the star product.
Let ![]() be the Weyl transforms of the operators
be the Weyl transforms of the operators ![]() .
Then the Weyl transform
.
Then the Weyl transform ![]() of the operator
of the operator ![]() is given
by the Moyal star product
is given
by the Moyal star product
![]() :
:
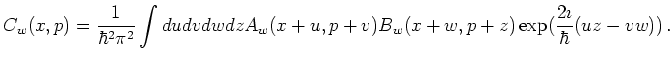 |
(6.49) |
The ![]() -multiplication of c-number phase space functions is in complete
isomorphism to Hilbert-space operator multiplication.
-multiplication of c-number phase space functions is in complete
isomorphism to Hilbert-space operator multiplication.
The von Neumann equation
![$\displaystyle \imath \hbar \frac{\partial \rho(x,t)}{\partial t} = [H, \rho(x,t)]$](img431.png) |
(6.50) |
![]()
![]()
![]()
![]() Previous: 6.2.2 Definition of Wigner
Up: 6.2 Quantum Mechanics in
Next: 6.2.4 Probabilistic Structure
Previous: 6.2.2 Definition of Wigner
Up: 6.2 Quantum Mechanics in
Next: 6.2.4 Probabilistic Structure