previous up next contents Previous: 6.2.5 A Caveat on Up: 6.2 Quantum Mechanics in Next: 6.2.7 Quantum Propagators and


6.2.6 A Feasible Phase Space Distribution

There are numerical issues with the Wigner transform so that we would like to avoid this task. Instead we will now define a distribution which in one dimension classically approximates the phase space distribution. We want our distribution to reproduce exactly the marginal expectation values for $ n(x)$, $ j(x)$ and $ E(x)$. Other local expectation values are not necessarily reproduced correctly.

Carrier, current, and energy marginal densities can be directly calculated from the Schrödinger function $ \psi(x)$ respectively the hydrodynamical quantities $ R,\tilde{S}$ with $ \psi = Re^{\imath \tilde{S}}$. Instead of the densities $ n(x), j(x), E(x)$ we prefer to work with the marginal $ x$-distributions for the in the case of constant mass equivalent set of ``local'' observables $ I, K = -\imath \partial_x, K^2 = (-i\partial_x)^2$, where $ I$ denotes the identity operator.

Introducing the variable

$\displaystyle a = - \imath (R' + \imath R \tilde{S}') ,$ (6.65)

we get the marginal expectation values (using the split of the energy operator as in Equation 6.63) for a pure state $ \rho = \vert\psi \rangle \langle \psi \vert$:

$\displaystyle I(x) $ $\displaystyle = R^2 ,$ (6.66)
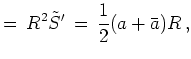$\displaystyle K(x) $ $\displaystyle = R^2 \tilde{S}' = \frac{1}{2}(a + \bar{a}) R ,$ (6.67)
$\displaystyle K^2(x)$ $\displaystyle = (R')^2 + (\tilde{S}'R)^2 = a \bar{a} ,$ (6.68)

To define a corresponding classical phase space distribution function $ w(x,p)$ we assume that for a wave function $ \psi$ the corresponding distribution w(x,p) for each $ x$ consists of left (up) and right (down) going modes, i.e.:

$\displaystyle w(x, p) = D(x) \delta(p - p(x)) + U(x) \delta(p + p(x))$ (6.69)

with $ p(x) \geq 0$.

This assumption makes sense in cases, in which the classical problem has a similar property. Such is the case for the scattering problems and the open Schrödinger equation which we consider in Section 7.1. In this case particles are injected with a fixed momentum $ p$ from one electrode and condition 6.70 is fulfilled exactly. In the electrodes we have a superposition of transmitted and reflected modes.

From the ansatz 6.70 we can calculate the classical quantities:

$\displaystyle I(x) $ $\displaystyle = U(x) + D(x) ,$ (6.70)
$\displaystyle K(x) $ $\displaystyle = -U(x) p(x) + D(x) p(x) $ (6.71)
$\displaystyle K^2(x)$ $\displaystyle = (U(x) + D(x)) p^2(x) .$ (6.72)

Classically $ U$ and $ D$ are always positive quantities. Equating the marginal expectation values from the wave function and from the ``classical'' distribution function $ w$ we get the system of equations:

$\displaystyle D + U = R^2 ,$ (6.73)

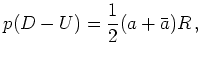$\displaystyle p (D - U) = \frac{1}{2}(a + \bar{a}) R ,$ (6.74)

$\displaystyle p^2(D + U) = a \bar{a} .$ (6.75)

From the last equation we get

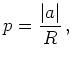$\displaystyle p = \frac{\vert a\vert}{R} ,$ (6.76)

which reduces the system of equations to

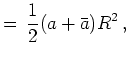$\displaystyle (D - U)\vert a\vert$ $\displaystyle = \frac{1}{2}(a + \bar{a})R^2 ,$ (6.77)
$\displaystyle D + U $ $\displaystyle = R^2 ,$ (6.78)

with the solution

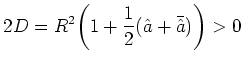$\displaystyle 2D = R^2 \bigg(1 + \frac{1}{2}(\hat{a} + \bar{\hat{a}})\bigg) > 0$ (6.79)

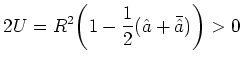$\displaystyle 2U = R^2 \bigg(1 - \frac{1}{2}(\hat{a} + \bar{\hat{a}})\bigg) > 0$ (6.80)

with

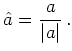$\displaystyle \hat{a} = \frac{a}{\vert a\vert} .$ (6.81)

The coefficients $ U$ and $ D$ are positive values between 0 and $ 1$ as has to be the case for proper probabilities. To sum up: Our (1+1)-dimensional distribution function has the property that it is positive and reproduces the moments up to an order $ \leq 2$ correctly.

previous up next contents Previous: 6.2.5 A Caveat on Up: 6.2 Quantum Mechanics in Next: 6.2.7 Quantum Propagators and

R. Kosik: Numerical Challenges on the Road to NanoTCAD