6.2.7 Quantum Propagators and Trajectories

Description of quantum phenomena in terms of particle trajectories is a promising approach for understanding and modeling the transport in nanoscale electronic devices.

In [TM98] the potential term has been interpreted as a quantum force giving rise to dynamic particle trajectories. They nicely explain the tunneling process but yet cannot solve Equation 6.52 because the quantum force itself depends on the solution $f_w$.

In [NDRJ96] a particle approach to the coherent Wigner equation has been proposed. The Wigner potential has been treated exactly by the iteration series of the equation. The convergence of the obtained backward Monte Carlo method has been theoretically investigated.

Recently the coherent Equation 6.52 has been solved numerically by using particles [SF01] which cross the device by collisionless drift over classical trajectories. The information about $V_w$ is retained as particle affinity.

The phase space propagator $L_t(x, p; x_0, p_0)$ is defined to give the time evolution of the Wigner function

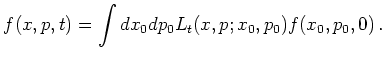$$f(x, p, t) = \int dx_0 dp_0 L_t(x, p; x_0, p_0) f(x_0, p_0, 0) .$$ (6.82)

Quantum propagators can be quite different from classical propagators. The classical equations of motion define classical trajectories in phase space for the coordinates $x(t)$, and momenta $p(t)$, as a function of the time $t$. The classical propagators for Liouville distributions in phase space are therefore $\delta$ functions over the classical trajectories defining a one-to-one mapping between single points of the initial and final distributions. In quantum mechanics, on the other hand, a single point of the phase space distribution at one time can in principle be causally connected to many points of this phase space distribution at any other time. Furthermore, quantum propagators may include quantum jumps, sudden changes in the momentum or quick change in the coordinate of the phase space quasi distributions. Two points of the phase space distribution at two different times can be causally connected even when no classical trajectory connects them. These are essential quantum features.

For any Hamiltonian $H = p^2/m + V(x)$ with potential energy $V(x)$ and constant mass $m$ that is, at most, quadratic in the coordinate $x$, the phase space propagator is a $\delta$ function on the classical paths. For the free propagator ($V(x) = 0$) we get

$$L_t(x, p; x_0, p_0) = \delta(p - p_0) \delta(x - x_0 - t p_0/m)$$ (6.83)

In this case the classical and quantum dynamics are basically the same as Wigner's integro-differential equation for quadratic potentials is equivalent to Liouville's classical equation with a constant force term. The main difference is in the initial conditions: In the quantum case the initial distribution must be chosen in such a way that it corresponds to a positive definite density matrix $\rho_0$. In the classical case any positive distribution function $f_0$ can be chosen.

For more complicated potentials the phase space propagator is no longer a $\delta$ function. To deal with this in a particle picture we develop a stochastic approach suitable for Monte Carlo methods in Chapter 9.