7.2.1 Separation of Neumann Equation

For the Hamiltonian 6.2 the von Neumann equation for the density matrix $\rho(x_1, x_2, t)$ reads

$$\imath \hbar \frac{\partial \rho}{\partial t} = [ H, \rho ]... ...^2} - \frac{{\partial}^2}{\partial{x_2}^2} ) \rho + (V(x_1) - V(x_2)) \rho .$$ (7.11)

To regain the Schrödinger equation from the von Neumann equation we make a separation ansatz for the density $\rho$:

$$\rho(x_1,x_2, t) = \psi(x_1, t) \phi(x_2, t).$$ (7.12)

We get (omitting $t$ in the function arguments)

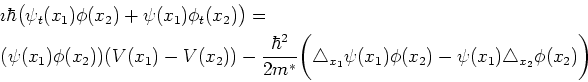$$\begin{gather*}\begin{split}& \imath \hbar \big(\psi_t(x_1) \phi(x_2) + \psi(x_1... ...) \phi(x_2) - \psi(x_1) \triangle_{x_2} \phi(x_2)\bigg) \end{split}\end{gather*}$$ (7.13)

Factoring out $\psi(x_1)$ and $\phi(x_2)$ gives

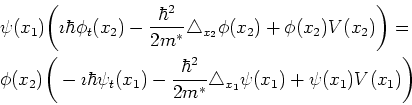$$\begin{gather*}\begin{split}&\psi(x_1)\bigg(\imath \hbar \phi_t(x_2) - \frac{\hb... ...{*}} \triangle_{x_1} \psi(x_1) + \psi(x_1) V(x_1)\bigg) \end{split}\end{gather*}$$ (7.14)

Division by $\psi(x_1)\phi(x_2)$ separates the equation and we get (with $E$ as separation constant)

$$\imath \hbar \psi_t(x_1) = - \frac{\hbar^2}{2m^{*}} \triangle_{x_1} \psi(x_1) + V(x_1) \psi(x_1) - E \psi(x_1) ,$$ (7.15)

$$\imath \hbar \phi_t(x_2) = \frac{\hbar^2}{2m^{*}} \triangle_{x_2} \phi(x_2) - V(x_2) \phi(x_2) + E \phi(x_2) .$$ (7.16)

If $\psi$ is a solution to Equation 7.15 with separation constant $E$, then $\psi^*$ is a solution to Equation 7.16 with complex conjugate separation constant $E^*$ and the density matrix $\rho$ is of the form $\psi(x_1) \psi^*(x_2)$ corresponding to a pure state.

We get an additional term $E\psi(x,t)$ in the separated equation, which is at first surprising since we are not in the stationary case. However, the von Neumann equation is invariant under a change of $V$ to $V + E$, while the Schrödinger equation is not.

By separation of the transient von Neumann equation we get the Schrödinger equation with an additional term $\tilde{E}\psi$. This shifts the value of $E$ in the stationary Schrödinger equation. But varying $E$ the set of solutions $\psi$ stays the same. So we can set $\tilde{E} = 0$ without loss of generality.