7.2.6.1 Schrödinger Equation with an Imaginary Potential

One way to describe dissipative effects in the Schrödinger equation is by introduction of an imaginary potential $\imath W_0$, also called an optical potential as it describes optical phonon scattering. This model is discussed in [SHMS98]. The time-dependent Schrödinger equation becomes

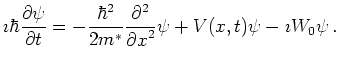$$\imath \hbar \frac{\partial \psi}{\partial t} = - \frac{\hbar^2}{... ...} \frac{{\partial}^2}{{\partial x}^2} \psi + V(x,t) \psi - \imath W_0 \psi .$$ (7.22)

As discussed in [SHMS98] in this model the current density is attenuated by the optical potential at a rate of $2W_0/\hbar$, which corresponds to a scattering time

$$\tau = \hbar/(2 W_0) .$$ (7.23)

As a first step in the construction of a scattering model we show the relation of this model with the model for relaxation time scattering in the Wigner method. Scattering in the relaxation time approximation is discussed in Section 8.1, Equations 8.1 and 8.3. In the density matrix picture this is the equation:

$$\imath \hbar \frac{\partial \rho}{\partial t} = [ H, \rho ] - \im... ...2})} {\rho^{\mathrm{eq}}(\frac{x_1 + x_2}{2},\frac{x_1 + x_2}{2})} \right) .$$ (7.24)

If we ignore the inscattering term we can separate this equation. We get

$$\begin{gather*}\begin{split}& \imath \hbar \psi_t(x_1) = - \frac{\hbar^2}{2m^{*}... ...i(x_2) - \frac{\imath \hbar}{2 \tau} + E \phi(x_2) . \end{split}\end{gather*}$$ (7.25)

As for the proper Schrödinger equation we get a pair of mutually complex conjugate equations. If we put $\hbar /(2 \tau) = W_0$ in 7.25 we see that Haddad's identification Equation 7.23 is correct. But we also see, that basically only outscattering is modeled by the introduced imaginary potential. We will identify and examine ways to include also inscattering into the QTBM in the next subsections.