previous up next contents Previous: 7.2.6.1 Schrödinger Equation with Up: 7.2.6 Scattering in the Next: 8. Finite Difference Wigner

7.2.6.2 Relaxation-Time-Like Models

Some of the proposed scatterings model are most conveniently described using the hydrodynamical formulation of quantum mechanics. To derive a model for inscattering we point out a superficial formal analogy between the Wigner density picture and the QTBM.

In the Wigner picture we have for each $ k$ a density $ f(x,k)$. In the QTBM we have for each $ k$ a mode $ \psi_k(x)$ and a corresponding hydro density

$\displaystyle n_k(x) = \vert\psi_k(x)\vert^2 = R_k^2(x) .$ (7.26)

This formal analogy is a guideline which was helpful in finding a scattering model for the use with the QTBM. It should not be stretched too far.

From the modes we build the mixed state

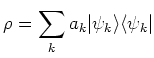$\displaystyle \rho = \sum_k a_k \vert\psi_k\rangle \langle \psi_k \vert$ (7.27)

with corresponding density

$\displaystyle n(x) = \rho(x,x) .$ (7.28)

We are not interested in Schrödinger models for relaxation time scattering per se, but it is a good test case and gives important hints on how to model scattering. We will propose a refined QTBM Schrödinger model for scattering which includes a better model for inscattering. The models proposed in this section share some properties with the Wigner relaxation time models. They are not identical in the sense of being equivalent via a Wigner transform, hence we call them ``relaxation-time-like''.

As a first proposal for a model of this type we try (using the anology above):

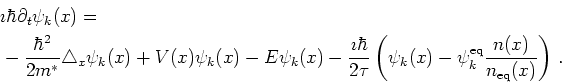\begin{gather*}\begin{split}& \imath \hbar \partial_t \psi_k(x) = & - \frac{\... ...mathrm{eq}} \frac{n(x)}{n_{\mathrm{eq}}(x)}\right) . \end{split}\end{gather*} (7.29)

This model has the property that for $ \tau \rightarrow 0$

$\displaystyle \psi_k(x) \rightarrow \psi_k^{\mathrm{eq}}(x) .$ (7.30)

However, the scattering term

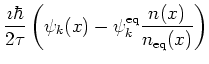$\displaystyle \frac{\imath \hbar}{2 \tau} \left(\psi_k(x) - \psi_k^{\mathrm{eq}} \frac{n(x)}{n_{\mathrm{eq}}(x)}\right)$ (7.31)

does not conserve mass for the corresponding mixed density $ n(x)$.

We will now look at the same problem in the hydrodynamical formulation which provides further insight. The Schrödinger equation with relaxation time outscattering becomes for a mode $ \psi_k$

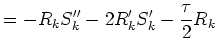$\displaystyle \partial_t R_k$ $\displaystyle = -R_k S_k'' - 2 R_k'S_k' - \frac{\tau}{2} R_k$ (7.32)
$\displaystyle \partial_t R_k^2$ $\displaystyle = -2 (R_k^2 S_k')' - \tau R_k^2 .$ (7.33)

Note that the equation for $ S_k$ stays unchanged. We obtain a modified continuity equation. The resulting current is no longer constant.

As a hydrodynamical relaxation time model which also includes inscattering we propose

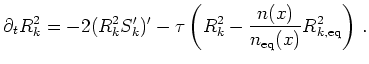$\displaystyle \partial_t R_k^2 = -2 (R_k^2 S_k')' - \tau \left(R_k^2 - \frac{n(x)}{n_{\mathrm{eq}}(x)}R_{k,\mathrm{eq}}^2\right) .$ (7.34)

The corresponding wave function scattering term is

$\displaystyle \frac{1}{2 \tau} \left( \psi_k - \frac{{\vert\psi_k^{\mathrm{eq}}\vert}^2}{\psi_k^{\star}} \frac{n(x)}{n_{\mathrm{eq}}(x)} \right) .$ (7.35)

This model does not relax $ \psi_k$, but only relaxes $ \vert\psi_k\vert$ towards the equilibrium values. We can relax left and right going modes separately or in parallel, in the last case we have

$\displaystyle n(x) = n_l(x) + n_r(x) . $

This model conserves mass. To compare it with the Wigner relaxation time model we look at the pure state

$\displaystyle \rho_k = \vert\psi_k \rangle \langle \psi_k\vert = \psi_k(x_1) \psi_k^*(x_2) .$ (7.36)

Using hydrodynamical variables this state is written as

$\displaystyle \rho_k(x_1, x_2) = R_k(x_1) e^{\imath S_k(x_1)/\hbar} R_k(x_2) e^... ...x_2)/\hbar} = \tilde{R_k}(x_1,x_2) e^{\imath \tilde{S_k}(x_1, x_2)/\hbar} . $

From the Schrödinger equation for $ \psi_k$ with scattering term 7.35 we derive a von Neumann equation for $ \rho_k$ where the scattering is of the form

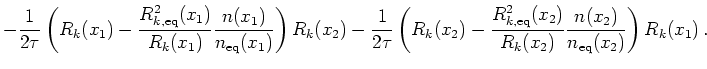$\displaystyle -\frac{1}{2\tau}\left( R_k(x_1) - \frac{R_{k,\mathrm{eq}}^{2}(x_1... ...}^{2}(x_2)}{R_k(x_2)} \frac{n(x_2)}{n_{\mathrm{eq}}(x_2)} \right) R_k(x_1) .$    

For the outscattering this gives

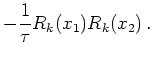
$\displaystyle - \frac{1}{\tau} R_k(x_1) R_k(x_2) . $

For the inscattering we get

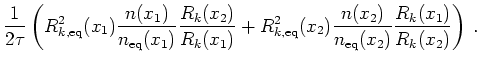
$\displaystyle \frac{1}{2 \tau} \left( R_{k,\mathrm{eq}}^{2}(x_1) \frac{n(x_1)... ...2) \frac{n(x_2)}{n_{\mathrm{eq}}(x_2)} \frac{R_k(x_1)}{R_k(x_2)} \right ) . $

The inscattering is not closed (that is, expressed by) in $ \tilde{R_k}(x_1, x_2) = R_k(x_1)R_k(x_2)$ and no equation closed in $ \rho_k$ is derived.

The inscattering from Wigner relaxation time scattering is (writing Equation 7.24 in hydro variables):

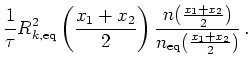$\displaystyle \frac{1}{\tau} R_{k,\mathrm{eq}}^2\left(\frac{x_1 + x_2}{2}\right) \frac{n(\frac{x_1 + x_2}{2})} {n_{\mathrm{eq}}(\frac{x_1 + x_2}{2})} .$ (7.37)

Comparing our proposed model for inscattering and the original Wigner relaxation time scattering we see that the QTBM hydro model approximates

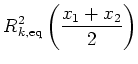
$\displaystyle R_{k,\mathrm{eq}}^2\left(\frac{x_1 + x_2}{2}\right) $

by

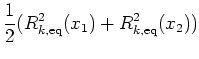
$\displaystyle \frac{1}{2}(R_{k,\mathrm{eq}}^2(x_1) + R_{k,\mathrm{eq}}^2(x_2)) $

and puts

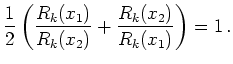$\displaystyle \frac{1}{2}\left ( \frac{R_k(x_1)}{R_k(x_2)} + \frac{R_k(x_2)}{R_k(x_1)} \right ) = 1 .$ (7.38)

The equation for $ \tilde{S}$ is the same in both cases, scattering does not enter.

Implementation of hydrodynamical models is a formidable task, see [Bit00] for related work. Our experience with the Riccati equation is also disheartening. Hence the numerical validation of all proposed scattering models is an open issue.

previous up next contents Previous: 7.2.6.1 Schrödinger Equation with Up: 7.2.6 Scattering in the Next: 8. Finite Difference Wigner

R. Kosik: Numerical Challenges on the Road to NanoTCAD