4.1 Allgemeine Betrachtungen




Next: 4.2 Die Momentenmethode
Up: 4 Verfahren zur Lösung
Previous: 4 Verfahren zur Lösung
Eine erste Schwierigkeit in Bezug auf die numerische Lösbarkeit
ergibt sich aus der hohen Dimension des Phasenraumes. Im stationären Fall
besitzt der (k,r) Raum 6 Dimensionen, beschränkt man sich auf
2 dimensionale Simulationsgebiete, bleibt immer noch ein 5 dimensionaler
Raum 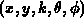 , den es zu diskretisieren gilt.
Beschränkt man sich auf ein eindimensionales Gebiet, so besitzt die
Verteilungsfunktion Zylindersymmetrie, und man kommt mit 3 Dimensionen
, den es zu diskretisieren gilt.
Beschränkt man sich auf ein eindimensionales Gebiet, so besitzt die
Verteilungsfunktion Zylindersymmetrie, und man kommt mit 3 Dimensionen
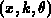 aus. Es soll hinzugefügt werden, daß Reduktion der
Dimension des Problems die Anzahl der praktisch anwendbaren Lösungsverfahren
vergrößert. Am einfachsten ist natürlich eine örtlich homogene Situation
zu behandeln, für deren Beschreibung 2 unabhängige Variablen
ausreichen
aus. Es soll hinzugefügt werden, daß Reduktion der
Dimension des Problems die Anzahl der praktisch anwendbaren Lösungsverfahren
vergrößert. Am einfachsten ist natürlich eine örtlich homogene Situation
zu behandeln, für deren Beschreibung 2 unabhängige Variablen
ausreichen 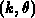 .
.
Neben der hohen Dimension des Problems erkennt man eine zweite Schwierigkeit,
wenn man das Streuintegral
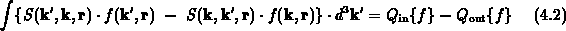
betrachtet. Durch Vergleich erkennt man, daß die beiden Operatoren
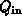 und
und 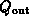 definiert sind als
definiert sind als
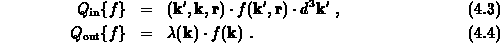
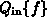 beschreibt die von allen erlaubten Zuständen
beschreibt die von allen erlaubten Zuständen 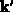 in den Zustand
in den Zustand 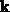 hineingestreuten Teilchen. Da es sich dabei um
einen Integraloperator handelt, muß zur Auswertung dieses Terms die gesamte
Verteilungsfunktion bekannt sein. Interpretiert man die Boltzmanngleichung als Kontinuitätsgleichung,
so bildet dieser Term eine Quelle im
hineingestreuten Teilchen. Da es sich dabei um
einen Integraloperator handelt, muß zur Auswertung dieses Terms die gesamte
Verteilungsfunktion bekannt sein. Interpretiert man die Boltzmanngleichung als Kontinuitätsgleichung,
so bildet dieser Term eine Quelle im 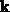 -Raum.
-Raum.
Der Operator  zur Beschreibung der aus dem Zustand
zur Beschreibung der aus dem Zustand
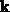 hinausgestreuten Teilchen ist ein einfacher Multiplikationsoperator,
der die Multiplikation mit der totale Streurate
hinausgestreuten Teilchen ist ein einfacher Multiplikationsoperator,
der die Multiplikation mit der totale Streurate 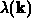 erfordert.
erfordert.
 geht mit negativem Vorzeichen ein und kann somit als Senke
interpretiert werden.
geht mit negativem Vorzeichen ein und kann somit als Senke
interpretiert werden.
Die Diskretisierung eines Integraloperators führt zu einer voll
besetzten Koeffizientenmatrix, anders als bei der Diskretisierung eines
Differentialoperators.
Der Wert der Verteilungsfunktion an einem Punkt hängt von den Werten an allen anderen
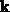 -Punkten ab und nicht mehr nur von den nächsten Nachbarn, wie es
bei Differentialgleichungen der Fall ist.
Eine diskrete Lösung der Boltzmanngleichung scheidet daher für zweidimensionale
Probleme auf Grund des enormen Speicherbedarfes aus.
Für konstantes Feld hingegen ist dieser direkte Lösungsweg gangbar
[45]. Auch eine Erweiterung für eindimensionale Probleme dürfte auf Grund
der oben angestellten Betrachtungen über die Anzahl der unabhängigen
Variablen realistisch sein.
-Punkten ab und nicht mehr nur von den nächsten Nachbarn, wie es
bei Differentialgleichungen der Fall ist.
Eine diskrete Lösung der Boltzmanngleichung scheidet daher für zweidimensionale
Probleme auf Grund des enormen Speicherbedarfes aus.
Für konstantes Feld hingegen ist dieser direkte Lösungsweg gangbar
[45]. Auch eine Erweiterung für eindimensionale Probleme dürfte auf Grund
der oben angestellten Betrachtungen über die Anzahl der unabhängigen
Variablen realistisch sein.
Die Schwierigkeiten, die der Integraloperator mit sich bringt, werden in
der Relaxationszeitnäherung umgangen.
Der Ansatz
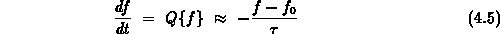
bewirkt, daß etwa unter homogenen Bedingungen eine Störung des
Elektronensystems in der Zeit exponentiell abklingt
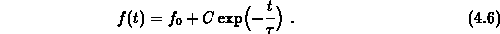
Dieser Ansatz ist aber nur dann hinreichend genau, wenn das elektrische Feld
klein ist und die Streuprozesse entweder elastisch oder isotrop sind
[64].
Nachdem in hochminiaturisierten Bauelementen gerade extremer
Nichtgleichgewichtstransport vorherrscht, erscheint diese Näherung für die
Modellierung doch als zu grob.
Eine gewisse historische Bedeutung hat der Ansatz einer verschobenen
Maxwell-Verteilung erlangt. Es konnten damit viele Effekte im
Zusammenhang mit dem nichtlinearen Transportverhalten in Verbindungshalbleitern
erfolgreich beschrieben werden. Aber auch diese Methode wird den heute
gestellten Anforderungen an die Bauelementesimulation nicht gerecht.
So weicht bereits bei einem starken homogenen Feld die Verteilungsfunktion
von der vorausgesetzten Form ab. Im stark inhomogenen Fall treten
zusätzliche Merkmale der Verteilungsfunktion auf, die in dem Ansatz nicht enthalten
sind.
Die ebenfalls schon länger bekannte Methode, die Verteilungsfunktion nach
Legendre-Polynomen
zu entwickeln, fand in jüngster Zeit Eingang in die eindimensionale
Bauelementesimulation. Auf Grund der Zylindersymmetrie
kann 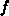 angesetzt werden als
angesetzt werden als
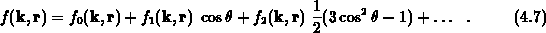
Der Abbruch der Reihe nach dem Glied 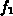 , wie er in
den in [2][61] beschriebenen Implementationen durchgeführt wird, scheint aber
doch eine grobe
Näherung bezüglich der Verteilungsfunktion zu sein.
, wie er in
den in [2][61] beschriebenen Implementationen durchgeführt wird, scheint aber
doch eine grobe
Näherung bezüglich der Verteilungsfunktion zu sein.
Eine sehr interessante Alternative stellt die relativ neue Methode dar,
die Boltzmanngleichung auf einen zellulären Automaten abzubilden
[55] [86].
Das Simulationsgebiet wird in Zellen unterteilt, wobei nur Wechselwirkungen
zwischen den nächsten Nachbarn auftreten. Dieses Verfahren ist ebenso wie
die Monte-Carlo-Methode stochastischer Natur. Als großer Vorteil ist zu
werten, daß dieser Algorithmus auf Parallelrechnern mit SIMD-Architektur
besonders effizient implementiert werden kann. Außerdem zeichnet sich
dieser Algorithmus durch besondere Robustheit aus.
Die Anwendung des Verfahrens ist derzeit auf Grund der uniformen Zellenstruktur
auf die Simulation von MESFETs beschränkt. Zur Simulation eines
MOSFETs ist wegen des Inversionskanals eine nichtuniforme Diskretisierung
unabdingbar.
Zur Modellierung des Nichtgleichgewichtstransportes in eindimensionalen
Strukturen wurde der sogenannte ,,Scattering Matrix Approach`` entwickelt
[20] [96]. Das Simulationsgebiet wird dabei in gleich große Scheiben unterteilt.
Weiters wird der Geschwindigkeitsraum diskretisiert, wobei jedem
Diskretisierungsgebiet ein Teilfluß zugeordnet wird. Die Streumatrix gibt nun
die Transmissions- und Reflexionswahrscheinlichkeiten für die
unterschiedlichen
Teilflüsse an. Ein eindimensionales Bauelement wird durch Serienschaltung
solcher Streumatrizen modelliert. Da dieses Verfahren deterministisch ist,
kann eine höhere Genauigkeit als mit stochastischen Methoden erzielt werden.
Die Streumatrizen müssen für ein Halbleitermodell
nur einmal berechnet werden und können dann wiederholt verwendet werden.
Die entsprechenden Bibliotheken werden allerdings sehr groß, da eine
Streumatrix als Parameter die Feldstärke und die Dotierung besitzt und ihre
Dimension von der Feinheit der Geschwindigkeitsdiskretisierung abhängt.
Obwohl empirisch gezeigt wurde, daß der ,,Scattering Matrix Approach`` die
gleichen nichtlokalen Transporteffekte wie die Monte-Carlo-Methode liefert,
steht ein Beweis für eine Äquivalenz zur Boltzmanngleichung noch aus.




Next: 4.2 Die Momentenmethode
Up: 4 Verfahren zur Lösung
Previous: 4 Verfahren zur Lösung
Martin Stiftinger
Wed Oct 12 11:59:33 MET 1994
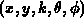 , den es zu diskretisieren gilt.
Beschränkt man sich auf ein eindimensionales Gebiet, so besitzt die
Verteilungsfunktion Zylindersymmetrie, und man kommt mit 3 Dimensionen
, den es zu diskretisieren gilt.
Beschränkt man sich auf ein eindimensionales Gebiet, so besitzt die
Verteilungsfunktion Zylindersymmetrie, und man kommt mit 3 Dimensionen
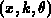 aus. Es soll hinzugefügt werden, daß Reduktion der
Dimension des Problems die Anzahl der praktisch anwendbaren Lösungsverfahren
vergrößert. Am einfachsten ist natürlich eine örtlich homogene Situation
zu behandeln, für deren Beschreibung 2 unabhängige Variablen
ausreichen
aus. Es soll hinzugefügt werden, daß Reduktion der
Dimension des Problems die Anzahl der praktisch anwendbaren Lösungsverfahren
vergrößert. Am einfachsten ist natürlich eine örtlich homogene Situation
zu behandeln, für deren Beschreibung 2 unabhängige Variablen
ausreichen 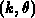 .
.




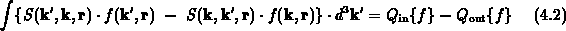
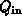 und
und 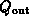 definiert sind als
definiert sind als
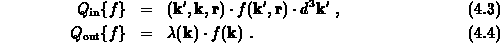
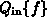 beschreibt die von allen erlaubten Zuständen
beschreibt die von allen erlaubten Zuständen 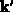 in den Zustand
in den Zustand 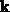 hineingestreuten Teilchen. Da es sich dabei um
einen Integraloperator handelt, muß zur Auswertung dieses Terms die gesamte
Verteilungsfunktion bekannt sein. Interpretiert man die Boltzmanngleichung als Kontinuitätsgleichung,
so bildet dieser Term eine Quelle im
hineingestreuten Teilchen. Da es sich dabei um
einen Integraloperator handelt, muß zur Auswertung dieses Terms die gesamte
Verteilungsfunktion bekannt sein. Interpretiert man die Boltzmanngleichung als Kontinuitätsgleichung,
so bildet dieser Term eine Quelle im  zur Beschreibung der aus dem Zustand
zur Beschreibung der aus dem Zustand
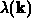 erfordert.
erfordert.
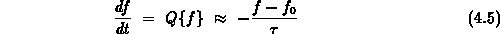
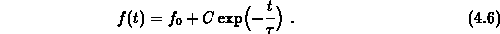
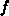 angesetzt werden als
angesetzt werden als
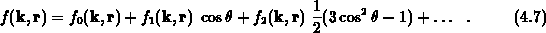
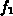 , wie er in
den in
, wie er in
den in