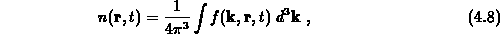
Wenn die Verteilungsfunktion bekannt ist, lassen sich die interessierenden makroskopischen Größen in einem Bauelement einfach ermitteln. So sind die primären Größen Trägerkonzentration und Stromdichte gegeben durch
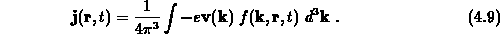
Als weitere Beispiele seien die Driftgeschwindigkeit und die mittlere Elektronenenergie angeführt,
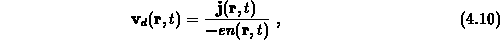
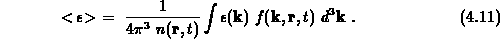
In vielen Fällen ist man an diesen Mittelwerten interessiert
und nicht an der zugrundeliegenden Verteilungsfunktion.
Gerade dieses Übermaß an Information,
das in der vollständigen Verteilungsfunktion enthalten ist, verursacht die
Schwierigkeiten, die mit der Lösung der Boltzmanngleichung verknüpft sind.
Mit Hilfe der Momentenmethode können Gleichungen für einzelne Mittelwerte
gezielt aufgestellt werden. Ist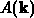 
eine Observable, an deren Mittelwert
man interessiert ist, so gelangt man durch Multiplikation der Boltzmanngleichung mit
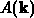und anschließender Integration über alle Wellenvektoren
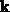zu der
Bestimmungsgleichung
wobei über gleichlautende Indizes summiert werden soll. Zur Umformung des ersten Terms auf der linken Seite wurde der Gaußsche Integralsatz verwendet und weiters angenommen, daß die Verteilungsfunktion im Unendlichen bzw. am Rand der Brillouinzone verschwindet.
Diese Gleichung hat die physikalische Bedeutung einer Bilanz- oder
Erhaltungsgleichung für
die Größe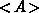 
. Üblicherweise setzt man für
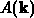aufsteigende Potenzen von 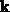oder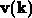 
ein und gelangt so zu einer
unendlichen Hierarchie von Momentengleichungen. Für die praktische Anwendung
muß diese Hierarchie
abgebrochen werden. Nachdem in eine Momentengleichung immer auch das
nächsthöhere Moment eingeht, muß beim Abbruch
für dieses letzte Moment ein physikalisch motivierter Ansatz getroffen
werden.
Aber auch diese endliche Menge von Momentengleichungen bildet noch kein
geschlossenes Gleichungssystem, sodaß weitere Näherungen erforderlich sind.
Eine Annahme besteht darin, tensorielle Größen durch Skalare,
üblicherweise wählt man die Spur des jeweiligen Tensors, zu approximieren.
Die nullte Momentengleichung beschreibt die Teilchenerhaltung. Setzt man
in die Gleichung 4.13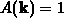 
ein, ergibt sich unmittelbar die
Kontinuitätsgleichung
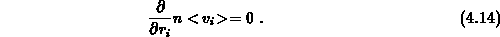
Da in der Boltzmanngleichung 4.1 Paargeneration und -rekombination nicht enthalten sind, ergibt die rechte Seite von 4.13 null.
Die in der Bauelementesimulation am häufigsten verwendeten Transportmodelle sind das Drift-Diffusionsmodell [67] [94] [110], welches die ersten beiden Momentengleichungen berücksichtigt, und das hydrodynamische Transportmodell. Von dem letzteren existieren zwei verschiedene Versionen. Dabei gehen entweder die ersten drei [3] [19] [22] [28] [29] [30] [31] [87] [88] oder die ersten vier [26] [34] [68] Momentengleichungen in das Transportmodell ein.
Bei der Herleitung dieser Transportmodelle wird in den allermeisten Fällen eine konstante effektive Masse vorausgesetzt, sodaß
gilt. Gerade diese Näherung wird häufig als wesentliche Einschränkung für die hydrodynamischen Transportmodelle gewertet. In neuere Arbeiten wird daher versucht, Nichtparabolizität in den Formalismus einzubeziehen [7] [15] [73] [98] [99].
Außerdem muß auf Grund der Notwendigkeit, ein geschlossenes System von Gleichungen zu erhalten, die rechte Seite jeder Bilanzgleichung 4.13 durch einen Relaxationszeitansatz
angenähert werden.
Darin bedeutet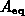 
den Mittelwert im thermodynamischen
Gleichgewicht.
Dieser Relaxationszeitansatz ist jedoch allgemeiner als jener in der
Boltzmanngleichung 4.5, da in den Momentengleichungen für jede
Observable 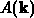eine ihr zugehörige Relaxationszeit
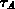definiert werden kann.
