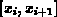Die selbstkonsistente Lösung von Monte-Carlo-Transport und Poissongleichung nach der Methode, die in
Abschnitt 6.3 beschrieben wird, erfordert zuzüglich die
Lösung der Halbleitergleichungen
[93].
Diese setzen sich aus der Poissongleichung und den
Kontinuitätsgleichungen für Elektronen und Löcher zusammensetzen.
Als Diskretisierungsverfahren für die Kontinuitätsgleichung zusammen mit
der klassischen Drift-Diffusionsstromgleichung 4.31 hat sich die
Scharfetter-Gummel-Methode [93] hervorragend bewährt.
Dabei wird angenommen, daß auf einer Geraden zwischen zwei Gitterpunkten
das elektrostatische Potential linear variiert und die Stromdichte konstant ist. Durch Lösen
der eindimensionalen Kontinuitätsgleichung in einem Diskretisierungsintervall
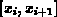gelangt man zu einer Interpolationsvorschrift für die
Trägerkonzentration.
Von Selberherr [35] stammt eine Erweiterung dieser Methode für nicht
konstantes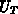 
, womit auch die erweiterte Stromgleichung 4.28
behandelt werden kann. Für die Temperaturspannung wird in Analogie zum elektrostatischen
Potential eine lineare Variation angenommen, wodurch, im Gegensatz zu
manchen publizierten Diskretisierungsverfahren, das Energie-Gradientenfeld konsistent
berücksichtigt wird.
Die eindimensionale Stromgleichung lautet für Elektronen
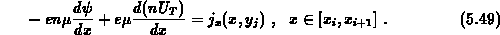
Die y-Koordinate sei konstant. Die Randbedingungen sind gegeben durch
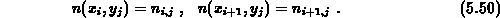
Die oben angeführten Annahmen, unter denen diese Differentialgleichung
nach 
gelöst wird, können in der Form
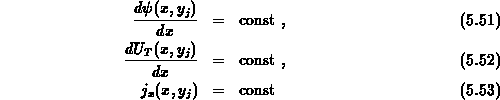
zusammengefaßt werden.
Die genaue Ableitung, die zu der im folgenden angegebenen diskreten Kontinuitätsgleichung führt, kann in [101] nachgelesen werden. Beschränkt man sich auf zwei Dimensionen, ergibt sich mit den Abkürzungen
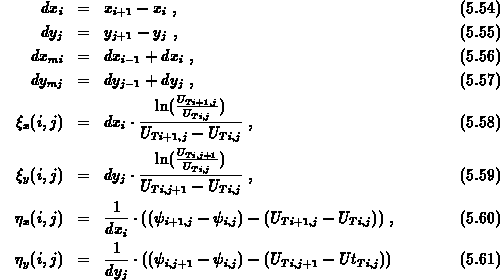
für die inneren Punkte bei Vernachlässigung der Paargeneration und -rekombination das Gleichungssystem 0.5
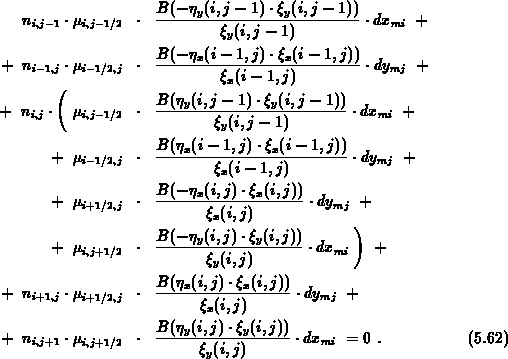
Darin bedeutet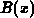 
die Bernoulli-Funktion
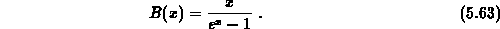
Nun soll noch der Grenzfall untersucht werden, daß die Temperaturspannung an allen Gitterpunkten gleich groß ist. Mit dem Grenzwert
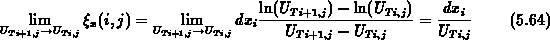
ergibt sich für den von 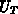abhängigen Term eines
Diskretisierungskoeffizientens
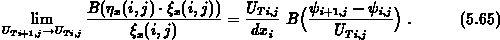
Das Argument in der Bernoulli-Funktion zeigt an, daß sich im
Grenzfall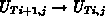 
genau die Scharfetter-Gummel-Diskretisierung
ergibt.