Next: 4.4.1 Gewähltes Integrationsverfahren Up: 4 Numerische Lösung der Previous: 4.3.2 Zeitableitungen und Generationsterme

4.4 Zeitintegration

Der betrachtete Differentialoperator 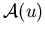$\mathcal{A}(u)$ aus Gl. 4.6 ist im Falle der Diffusionsgleichung mit

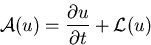$\begin{displaymath}\mathcal{A}(u)={\frac{\partial{u}}{\partial{t}}} + \mathcal{L}(u) \end{displaymath}$

(4.15)

gegeben, wobei 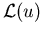$\mathcal{L}(u)$ nur Ableitungen nach den Ortskoordinaten enthält.

Diskretisiert man Gl. 4.6 nach den Ortskoordinaten, erhält man ein System gewöhnlicher Differentialgleichungen erster Ordnung entsprechend Gl. 4.11, welches sich zusammengefaßt durch

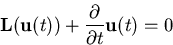$\begin{displaymath} \mathbf {L}(\mathbf {u}(t)) + {\frac{\partial{}}{\partial{t}}}\mathbf {u}(t) = 0 \end{displaymath}$

(4.16)

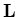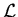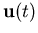wiedergeben läßt. $\mathbf {L}$ bezeichnet hier den Differentialoperator $\mathcal{L}$ in diskretisierter Form und $\mathbf {u}(t)$ ist der Vektor der zeitlichen Verläufe der Werte an den Knoten. Diese semi-diskretisierte Form von Gl. 4.6 läßt sich mit Hilfe verschiedener Methoden numerisch nach der Zeit integrieren [Vem81].

Ernst Leitner
1997-12-30