next up previous contents
Next: 6.2.3 Verbesserung der Methode Up: 6.2 Implementierte Fehlerabschätzung Previous: 6.2.1 Fehlerabschätzung nach Zienkiewicz

6.2.2 Eigenschaften der Methode

Technologisch relevante Dotierungsprofile weisen in der Regel eine sehr hohe Dynamik in ihrem Wertebereich auf. So liegen die Maximalwerte um einen Faktor 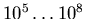$10^5 \ldots 10^8$ über den relevanten Minimalwerten. Demgemäß schwanken auch die lokalen Werte der Residuen. Um auch in Bereichen niedriger Konzentrationen eine brauchbare Fehlerabschätzung zu erhalten, muß Gl. 6.7 fast exakt gelöst werden. Das Iterationsverfahren nach Gl. 6.9 benötigt dazu leider zu viele Iterationen. Abb. 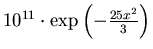6.2 zeigt das Ergebnis der Fehlerabschätzung anhand einer Gauß-Verteilung entsprechend $10^{11} \cdot \exp\left({-\frac{25x^2}{3}}\right)$ anhand einer Diskretisierung mittels 33 Stützstellen für unterschiedlich viele Iterationen.

  
Abbildung 6.2: Vergleich der Fehlerabschätzung mit dem exakten Diskretisierungsfehler für unterschiedliche Anzahl an Gauß-Seidel-Iterationen bei 33 Stützstellen.
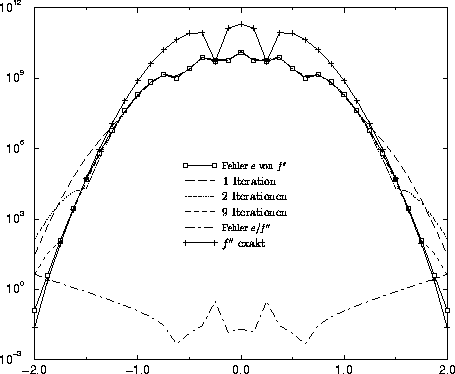\begin{figure} \vspace{-1.5cm} \psfrag{d2f_error}{\largeexakter Fehler $e$\spa... ...idth}{\textwidth}{\includegraphics{low.eps}}} } \vspace{-0.5cm}\par\end{figure}

Zur Veranschaulichung des Diskretisierungsfehlers wurde der Absolutwert des Diskretisierungsfehlers im logarithmischen Maßstab dargestellt, sodaß die Leistungsfähigkeit der Fehlerabschätzung im gesamten Wertebereich erkennbar wird. Mit zunehmender Dynamik des Wertebereiches werden somit immer mehr Iterationen nötig, damit die Fehlerabschätzung auch in den niedrigen Wertebereichen hinreichende Ergebnisse liefert. Allein deswegen kann diese Methode praktisch nicht in der gezeigten Art eingesetzt werden. Bei Versuchen mit größerem Stützstellenabstand zeigt sich weiters, daß die Abschätzung auch bei exakter Lösung von Gl. 6.7 in niedrigen Wertebereichen völlig unbrauchbar wird.
  
Abbildung 6.3: Qualität der Fehlerabschätzung bei unterschiedlicher Anzahl an Gauß-Seidel-Iterationen für größeren Stützstellenabstand (33 Stützstellen).
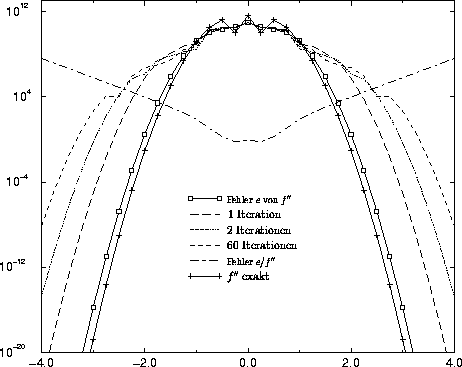\begin{figure} \vspace{-1.5cm} \psfrag{d2f_error}{\largeexakter Fehler $e$\spa... ...dth}{\textwidth}{\includegraphics{high.eps}}} } \vspace{-0.5cm}\par\end{figure}

Abb. 6.3 zeigt das Ergebnis der Fehlerabschätzung nach drei beziehungsweise 60 Gauß-Seidel Iterationen, wobei letzteres einer exakten Lösung von Gl. 6.7 gleichgesetzt werden kann. Die Aussagekraft des Kriteriums beschränkt sich auf wenige Größenordnungen im oberen Bereich. Darunter ist keine Relation zwischen dem tatsächlichen Diskretisierungsfehler und der Abschätzung erkennbar.

Die zumindest größenordnungsmäßige Kenntnis des Fehlers ist jedoch speziell in Gebieten niedriger Konzentrationen besonders wichtig, da genau dort viele Gitterpunkte eingespart werden können. Die Bewertung des Diskretisierungsfehlers muß allerdings relativ zum lokalen Funktionswert erfolgen. Eine falsche Größenordnung des abgeschätzten Diskretisierungsfehlers würde daher auch zu einer falschen Größenordnung der Gitterdichte führen.

Die dargestellte Fehlerabschätzung berücksichtigt diesen Entkopplungsmechanismus jedoch nicht, sondern bewertet die Einflüsse der benachbarten Werte gleich stark. Dadurch kommt es zur ``Überschwemmung'' von Gebieten niedriger Konzentration mit Diskretisierungsfehlern, die aus Gebieten mit hoher Konzentration stammen. Die Methode ist also dahingehend zu verbessern.

next up previous contents
Next: 6.2.3 Verbesserung der Methode Up: 6.2 Implementierte Fehlerabschätzung Previous: 6.2.1 Fehlerabschätzung nach Zienkiewicz
Ernst Leitner
1997-12-30