next up previous contents
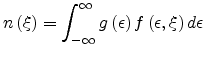
Next: 3.3 Results and Discussion Up: 3. The Effect of Previous: 3.1 Introduction

3.2 Theory

In the original transport energy model [10], the downward hopping transport and the effect of degenerate statistics were neglected. An electron with energy 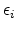$ \epsilon_i$, can only hop to a free localized state. In variable range hopping (VRH) theory, the numbers of empty sites enclosed by the contour $ R$ can be determined by the following equation [19].

$\displaystyle N\left(T,\beta,R,\epsilon'_i\right)=\int_0^{\pi}\int_0^{R}\int_{-... ...j\right)\right]\frac{1}{8\alpha^3} 2\pi R^{'2}\sin\theta d\epsilon'_jdR'd\theta$    

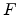Here $ F$ is the Fermi-Dirac distribution function, and 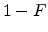$ 1-F$ is the probability that the finial site is empty. The Gaussian DOS is rewritten as

$\displaystyle g\left(\epsilon\right)=\frac{N_t}{\sqrt{2\pi}\cdot{a}}\exp\left[-\left(\frac{\epsilon-\epsilon_0}{\sqrt{2}\cdot{a}}\right)^2\right],$ (3.5)

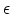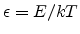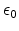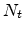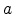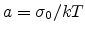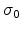where $ \epsilon$ is the normalized energy $ \epsilon=E/{kT}$, $ \epsilon_0$ is the Gaussian center, $ N_t$ is the effective DOS and $ a$ is defined as $ a=\sigma_0/{kT}$, where $ \sigma_0$ is the standard deviation of the Gaussian distribution. If we let 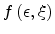$ f\left(\epsilon,\xi\right)$ be the normalized Fermi-Dirac distribution function, then the carrier concentration can be written as

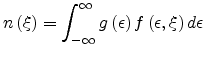$\displaystyle n\left(\xi\right)=\int_{-\infty}^\infty g\left(\epsilon\right)f\left(\epsilon,\xi\right)d\epsilon$ (3.6)

Considering the distribution function, 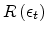$ R\left(\epsilon_t\right)$ will be calculated as

$\displaystyle R\left(E_t\right)=\left[\frac{4\pi}{3}\int_{-\infty}^{\epsilon_t} g\left(E\right)\left(1-f\left(\epsilon,\xi\right)\right)d\epsilon\right]^{-1/3}.$ (3.7)

Substituting (3.7) into (3.3), we obtain

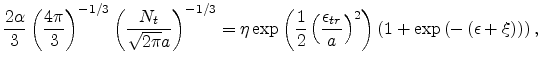$\displaystyle \frac{2\alpha}{3}\left(\frac{4\pi}{3}\right)^{-1/3}\left(\frac{N_... ...}{a}\right)^2\right)\left(1+\exp\left(-\left(\epsilon+\xi\right)\right)\right),$ (3.8)

where

$\displaystyle \eta=\left[\int_{-\infty}^{\epsilon_{t}}\frac{\exp\left(-\frac{1}... ...\right)d\epsilon} {1+\exp\left(-\left(\epsilon+\xi\right)\right)}\right]^{4/3}.$ (3.9)

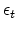$ \epsilon_{t}$ is the new transport energy and can be calculated by solving (3.9) numerically.

next up previous contents
Next: 3.3 Results and Discussion Up: 3. The Effect of Previous: 3.1 Introduction
Ling Li: Charge Transport in Organic Semiconductor Materials and Devices