


Next: 5.2 Diffusion Controlled Injection
Up: 5. Charge Injection Models
Previous: 5. Charge Injection Models
Over the past fifteen years, there has been a surge of interest in the
development and application of organic semiconductors, such as
organic light-emitting diodes (OLED) and organic field effect
transistors [25,105]. The processes of charge injection and
transport play an extremely important role for OLED. Metal electrodes inject
electrons and holes into opposite sides of the emissive organic layer(s), and
this injection process, in most cases, governs the overall efficiency of the
device. However, on the theoretical side there is still a lack of satisfactory
description of the physical process underlying the charge injection in organic
light-emitting diodes. One difficulty in extending our knowledge from
crystalline to amorphous organic semiconductors arises because charge transport
occurs no longer by free
propagation in extended states, but rather by hopping in a manifold of
localized states. This is reflected in the fact that there is little
theoretical work that gives the electrical current at the interface in terms
of experimentally obtainable parameters. Another difficulty arises from the fact
that the nature of the interface in terms of composition and structure is not
always understood. The sample preparation conditions, for example, have been
shown to have a dramatic influence on charge injection.
The barrier height that controls hole or electron injection plays an important
role in determining a measured current to be injection limited or transport
limited, such as trapped charge limited transport [106,107] or
space-charge-limited (SCL) transport with a field and temperature-dependent
mobility [108]. The SCL transport needs the injection barrier to be Ohmic,
i.e. it must be able to supply more carriers per unit time than the sample can
transport [109], which requires the injection barrier to be small enough. The
bulk-limited model predicts a dependence of the current density 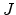 on the thickness
on the thickness
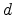 following
following
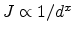
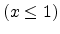 at a constant
field, where
at a constant
field, where 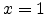 in the absence of deep trap (Child's law). In the
presence of an exponential distribution of traps,
in the absence of deep trap (Child's law). In the
presence of an exponential distribution of traps, 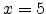 [110].
[110].
The present work is concerned with injection-limited conduction at high
electric field. The text book models to describe injection into a
semiconductor are the Fowler-Nordheim (FN) model for tunneling injection
and the Richardson-Schottky (RS) model for thermionic emission
[111]. The FN model ignores image charge effect and invokes
tunneling of electrons from a metal through a triangular barrier into unbound
continuum states. It predicts a current independent of temperature.
Here 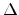 is the barrier height in the absence
of both the external field and the image effect,
is the barrier height in the absence
of both the external field and the image effect, 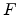 is the external field and
is the external field and 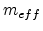 is the effective mass of the
carriers in the semiconductor. The RS model is based on the assumption that an
electron from the metal can be injected once it has acquired a thermal energy
sufficient to cross the potential maximum that results from the superposition
of the external and the image charge potential. The
is the effective mass of the
carriers in the semiconductor. The RS model is based on the assumption that an
electron from the metal can be injected once it has acquired a thermal energy
sufficient to cross the potential maximum that results from the superposition
of the external and the image charge potential. The
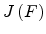 characteristic is predicted as
characteristic is predicted as
where
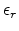 is the relative dielectric constant
. These two models, however, are insufficient to handle disordered
organic materials, where the density of states is a Gaussian
distribution, with localized carriers and discrete hopping
within a distribution of energy states [9]. Arkhipov presented an
analytical model based on hopping theory [112] and Wolf
performed detailed Monte Carlo simulations of charge injection from a
metal to an organic semiconductor layer [113]. In this chapter we will
present two injection models, one is based on drift-diffusion theory and the
other on a master equation.
is the relative dielectric constant
. These two models, however, are insufficient to handle disordered
organic materials, where the density of states is a Gaussian
distribution, with localized carriers and discrete hopping
within a distribution of energy states [9]. Arkhipov presented an
analytical model based on hopping theory [112] and Wolf
performed detailed Monte Carlo simulations of charge injection from a
metal to an organic semiconductor layer [113]. In this chapter we will
present two injection models, one is based on drift-diffusion theory and the
other on a master equation.



Next: 5.2 Diffusion Controlled Injection
Up: 5. Charge Injection Models
Previous: 5. Charge Injection Models
Ling Li: Charge Transport in Organic Semiconductor Materials and Devices
![]() on the thickness
on the thickness
![]() following
following
![]()
![]() at a constant
field, where
at a constant
field, where ![]() in the absence of deep trap (Child's law). In the
presence of an exponential distribution of traps,
in the absence of deep trap (Child's law). In the
presence of an exponential distribution of traps, ![]() [110].
[110].
![$\displaystyle J\left(F\right)=BF^2\exp\left[-\frac{4\left(2m_{eff}\right)^{1/2}\Delta^{3/2}}{3\hbar qF}\right].$](img437.png)
![$\displaystyle J\left(F\right)=CT^2\exp\left[-\frac{\left(\Delta-\left(\frac{q^3F}{4\pi\epsilon_r\epsilon_0}\right)^{1/2}\right)}{k_BT}\right],$](img439.png)