5.1 Phonons

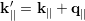
In second quantization, the vibrations are treated as quasi particles which are the phonons with an energy E = ℏω_q and a momentum p = ℏq. In the course of an interaction between an electron with energy E and a phonon with energy ℏω_q, the electron either emits or absorbs a phonon and the final electron energy is given by E^′ = E ± ℏω_q. In heterostructures the two dimensional wave vectors are conserved according to

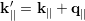where k _∥ and k_∥^′ are the in-plane wave vectors of the electron before and after the electron-phonon collision. The energy and momentum conservation reveals the particle nature of the phonons.

A distinction is drawn between acoustic and optical phonons. Acoustic phonons correspond to sound waves in a crystal lattice. Here, all atoms belonging to a basis system move in phase and the acoustic phonons have frequencies that become small at the long wavelengths  [82]. In the case of optical phonons, the atoms belonging to a basis system move out of phase and the oscillation frequencies are in the range of infrared and the visible spectrum. Optical phonons always have some minimum frequency of vibration, independent from the largeness of the wavelength.

In thermal equilibrium, the average number of phonons N_q is given by the Bose-Einstein distribution

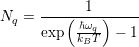(5.1)